The limit of the maximum of a sum of sines

Question

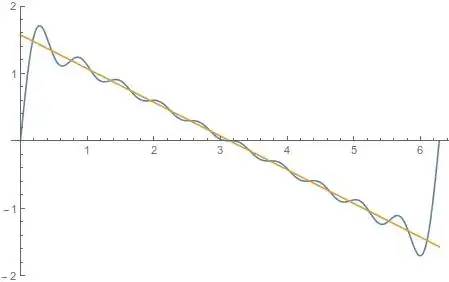
I've recently stumbled upon the following problem from Brilliant:

Compute the following:

$$\lim_{n\to\infty}\max_{x\in[0,\pi]}\sum_{k=1}^n\frac{\sin(kx)}k$$

Options:

1. $\displaystyle\int_0^\pi\frac{\cos^2(x)}{x^2}~\mathrm dx$

2. $\displaystyle\int_0^\pi\frac{\sin^2(x)}{x^2}~\mathrm dx$

3. $\displaystyle\int_0^\pi\frac{\sin(x)}x~\mathrm dx$

4. $\displaystyle\int_0^\pi\frac{\cos(x)}x~\mathrm dx$

Already by looking at it, it doesn't make sense for 1 or 4 to be correct, since they both diverge. Instinct then tells me the answer should be 3, since $\sin^2$ doesn't appear in the problem. However, I haven't been able to get to it.

By differentiating, I can find potential maxima as follows:

$$\frac{\mathrm d}{\mathrm dx}\sum_{k=1}^n\frac{\sin(kx)}k=\sum_{k=1}^n\cos(kx)=\csc\left(\frac x2\right)\sin\left(\frac{nx}2\right)\cos\left(\frac{(n+1)x}2\right)$$

Obviously the sum is zero on the boundaries, so we are not interested in them. Aside from them though, there are a lot of points to consider. My suspicion is that the maximum occurs at $x=\frac\pi{n+1}$ since this point has every term in the summand being positive. Furthermore, if this is the case, then we can rearrange the original sum into a Riemann sum, getting 3 as the answer.

How may we continue? Or perhaps this is the wrong approach...?

---

One may also note that answer choice 2 is less than answer choice 3, and we can see 3 is a possible answer choice, meaning that if this exists and is one of the answer choices, it must be the 3rd one.

Answer 1

The series

$$ S_n(x) = \sum_{k=1}^n \frac{\sin(k x)}{x} $$

represent in the Fourier sense, limiting approximations for the periodic piecewise function

$$ f(x) = \frac{\pi}{2}-\frac x2, \ \ \ 0\le x \lt 2\pi $$

So we have

$$ \lim_{n\to\infty}\left(\max_{0\le x\le \pi}\sum_{k=1}^n\frac{\sin(k x)}{k}\right) = \frac{\pi}{2}+\delta $$

here $\delta$ is due to the Gibbs phenomenon which can be calculated as

$$ \delta = 0.08948987223608363511601442291245487...\times \pi $$

where $\pi$ is the discontinuity jump value.

This result is the same of

$$ \int_0^{\pi}\frac{\sin x}{x} dx = 1.851937051982466... $$

Attached a plot with $n = 10$

Answer 2

The following proof is the main parts of $0<\sum_{k=1}^n\frac{\sin kx}{k}<\int_{0}^{\pi}\frac{\sin x}{x}dx$ posted by me.

Let $$f_n(x)=\sum_{k=1}^n\frac{\sin kx}{k},\quad x\in[0,\pi],$$ we can deal with as follows: consider $$f'_n(x)=\sum_{k=1}^{n}\cos kx=\frac{\cos\frac{n+1}{2}x\sin\frac{n}{2}x}{\sin \frac{x}{2}},x\in(0,\pi),$$ then $$f'_n(x)=0\iff \cos\frac{n+1}{2}x\sin\frac{n}{2}x=0,\quad x\in(0,\pi),$$ the critical points contained in $(0,\pi)$ of $f_n$ are listed below: $$\text{critical points}:\frac{\pi}{n+1}<\frac{2\pi}{n}<\frac{3\pi}{n+1}<\cdots.$$ Remark：The number of critical points of $f_n$ is $n$ if $n$ is odd, and is $n-1$ if $n$ is even. It can be shown that $$f_n\left(\frac{\pi}{n+1}\right)=\sum_{k=1}^n\frac{\sin\left(\frac{k\pi}{n+1}\right)}{k} =\max_{x\in[0,\pi]}f_n(x).$$

We get that: $$\sum_{k=1}^n\frac{\sin\left(\frac{k\pi}{n+1}\right)}{k} =\frac{1}{n+1}\sum_{k=1}^n\frac{\sin\left(\frac{k\pi}{n+1}\right)}{\frac{k}{n+1}}\to \int_{0}^{\pi}\frac{\sin x}{x}dx. \quad (\text{Riemann sum})$$