We know that 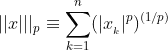 .
I am trying to figure out how to prove when p goes to infinity then the norm represent the maximum value of the vector
.
I am trying to figure out how to prove when p goes to infinity then the norm represent the maximum value of the vector
- 325
- 5
- 14
-
https://math.stackexchange.com/questions/326172/the-l-infty-norm-is-equal-to-the-limit-of-the-lp-norms/326266 – angryavian Feb 03 '19 at 22:20
-
2@angryavian the question you refer to deals with $\mathcal{l}_p$ norms of infinite sequences. The question here is for vectors in finite dimensional space. Much simpler, the spirit being the same – marwalix Feb 03 '19 at 22:31
1 Answers
Assume without loss of generality that $0 \leq x_1 \leq x_2 \leq \dots \leq x_n$. (Can you see why?)
If $x_n = 0$, you are done, as $$ \forall p\geq 1, \qquad 0=\lVert x\rVert_p \xrightarrow[p\to\infty]{} 0 = x_n $$
Otherwise, $x_n >0$, and we have $$ \forall p\geq 1, \qquad \lVert x\rVert_p = x_n\left( \sum_{k=1}^{n} \left(\frac{x_k}{x_n}\right)^p \right)^{1/p} = x_n\left( 1+ \sum_{k=1}^{n-1} \left(\frac{x_k}{x_n}\right)^p \right)^{1/p} $$ Since $0 \leq \frac{x_k}{x_n} \leq 1$ for all $1\leq k\leq n-1$, we therefore have, $\forall p\geq 1$, $$ x_n = x_n \cdot 1^{1/p} \leq \lVert x\rVert_p \leq x_n\cdot (n\cdot 1)^{1/p} = x_n \cdot n^{1/p} $$ and, as $p\to\infty$, by the squeeze theorem we get $\lim_{p\to\infty} \lVert x\rVert_p = x_n$, as claimed.
- 68,437