A simple euclidean geometry problem of angles of a triangle using linear equations

Question

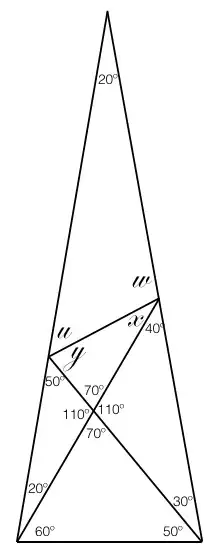
I am having problems solving this problem:

Using only basic geometry is easy to go here:

And propose 4 equations: $$ x+y+70=180$$ $$x+w+40=180 $$ $$u+y+50=180 $$ $$u+w+20=180 $$ And it doesn't make sense to me because, they are linear dependent, we can reduce it to 3 equations that depends (for example) of $u$.Giving us: $$y=130-u$$ $$w=160-u $$ $$x=u-20 $$

But for the construction of the problem, it don't understand how can this problem depends of a variable, and don't know how to solve it. Please help with this.

Answer 1

Let in $\Delta ABC$ we have $BA=BC$ and $\measuredangle ABC=20^{\circ}.$

Also, let $M\in BA$ and $N\in BC$ such that $\measuredangle BCM=20^{\circ}$ and $\measuredangle NAB=30^{\circ}.$

We need to find $\measuredangle NMC$ and $\measuredangle MNA$.

Indeed, let $K\in BN$ such that $KM||AC$ and let $AK\cap CM=\{L\}.$

Thus, $\Delta ACL$ and $\Delta KML$ they are equilateral triangles, which gives $$NC=AC=CL$$ and since $\measuredangle NCL=20^{\circ},$ we obtain $$\measuredangle CNL=\measuredangle NCL=80^{\circ},$$ which gives $$\measuredangle NLK=\measuredangle NKM-\measuredangle KLM=100^{\circ}-60^{\circ}=40^{\circ}.$$ In another hand, $$\measuredangle NKL=\measuredangle NKM-\measuredangle LKM=100^{\circ}-60^{\circ}=40^{\circ},$$ which gives $$NK=NL$$ and since $$MK=ML,$$ we obtain that $$\Delta NKM\cong\Delta NLM,$$ which gives $$x=\measuredangle NML=\frac{1}{2}\measuredangle KML=\frac{1}{2}\cdot60^{\circ}=30^{\circ}$$ and from here $$y=110^{\circ}-30^{\circ}=80^{\circ}.$$