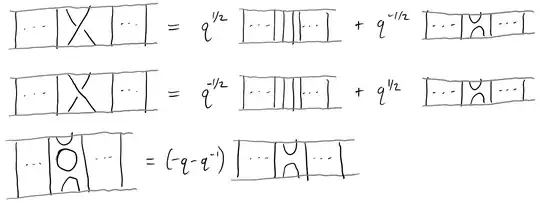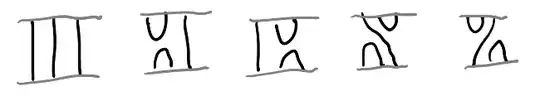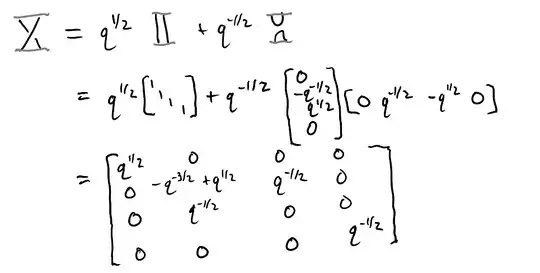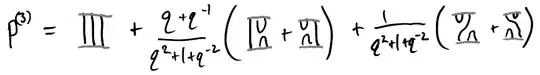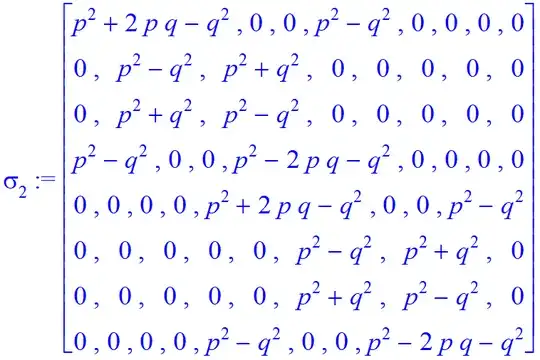$\mathbb{C}^2 \otimes \mathbb{C}^2 \otimes \mathbb{C}^2$ representation of $B_3$ braid group

Question

I've been trying to find a representation of the braid group $B_3$ acting on $\mathbb{C}^2 \otimes \mathbb{C}^2 \otimes \mathbb{C}^2$ but I can't find it anywhere.

From what I understand I have to find two $8 \times 8$ matrices $\sigma_i$ satisfying $\sigma_1 \sigma_2 \sigma_1 = \sigma_2 \sigma_1 \sigma_2$. I tried doing it by hand but it proved to be harder than anticipated. Is there any known solution to this?

Thanks!

By now I've looked into a mixture of readable books and papers I could find (I'm a physicists, the majority of the hardcore mathematical literature is unreadable to me). Do you have some good suggestion? — GKiu, Feb 03 '19 at 11:13
There is a homomorphism $B_3 \to S_3$, the symmetric group on 3 letters, and if $V$ is a vector space then $S_3$ acts on $V \otimes V \otimes V$, acting on simple tensors by permuting the factors: eg $(123) \cdot a \otimes b \otimes c = c \otimes a \otimes b$. This gives a representation of $B_3$ using the above homomorphism. If you don't want any non-trivial elements of $B_3$ to give the identity matrix, you want to ask that your representation is "faithful". — , Feb 03 '19 at 14:10
Thank you for your answer, and for putting it in simple terms. I understand how $S_3$ would act on the three letters, but how would $\mathbb{C}^2$ be incorporated in this? — GKiu, Feb 03 '19 at 19:03
It is a vector space and is otherwise irrelevant. You could replace it with $\Bbb R$. (This is why I think you should probably give some details about what you want to demand of this representation: I suspect this is not what you want.) — , Feb 03 '19 at 20:02
If you wanted the individual factors to matter you could also use the projection suggested by @Mike and take the $2$-dimensional irreducible rep for $S_3$, then tensor that with itself twice. But once again, it is not clear if this would really be the sort of thing you are looking for. — Tobias Kildetoft, Feb 03 '19 at 21:27

Kyle Miller · Accepted Answer · 2019-02-04T00:07:02.540

I'm going to make a guess that the motivation for your question is representations of $B_n$ that commute with representations of "quantum $\mathfrak{sl}(2)$." In this case, $\mathbb{C}^2$ would be the two-dimensional irreducible representation of $U_q(\mathfrak{sl}(2))$, known as $V_1$ since it is the highest-weight $1$ representation.

One may conceptualize this as looking for maps from $B_n$ to the space of endomorphisms of $(\mathbb{C}^2)^{\otimes n}$ that commute with the $\mathcal{U}_q(\mathfrak{sl}(2))$-action, where this quantum group is acting on each $\mathbb{C}^2$ factor simultaneously. That is, maps $B_n\to \operatorname{End}_{\mathcal{U}_q(\mathfrak{sl}(2))}(V_1^{\otimes n})$.

The $q=1$ case is the representation Mike Miller came up with: $B_3$ acts on $V_1^{\otimes 3}$ by permuting the tensor factors via the $B_3\to S_3$ homomorphism, and this intertwines with $(v_1\otimes v_2\otimes v_3) x=xv_1\otimes x v_2\otimes x v_3$ for $x\in\mathfrak{sl}(2)$, where $xv_i$ is simply the matrix-vector product.

More generally, we need to know the "$R$-matrix" for how a two-strand twist of $B_3$ corresponds to a homomorphism $V_1\otimes V_1\to V_1\otimes V_1$. The earlier conceptualization leads us to the Temperley-Lieb algebra, which for our purposes we will take $q\in\mathbb{C}^\times$ and then take $\mathbb{C}[B_n]$ and quotient it by (i.e., impose) the following relations:

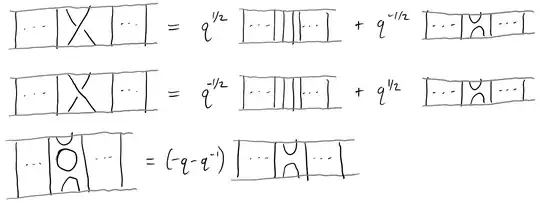
One can check that these satisfy the relations for $B_n$, and so this is a well-defined quotient. So: given a braid in $B_n$, one may resolve all crossings and expand the word into a linear combination of crossing-free Temperley-Lieb diagrams. For $B_3$, every braid reduces to a linear combination of the following five diagrams:

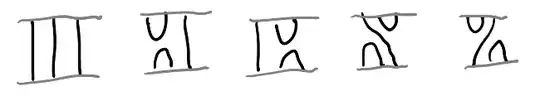
At this point, we can make a representation by deciding what "cups" and "caps" should be. According to some notes I have, the following choice works, where $\{e_1,e_2\}$ forms a basis for $\mathbb{C}^2$ and $\{e^1,e^2\}$ forms a corresponding dual basis for $(\mathbb{C}^2)^*$:

If I calculated it correctly, this is the two-strand twist as a matrix (derived from an $R$-matrix), with basis $\{e_{11},e_{12},e_{21},e_{22}\}$:

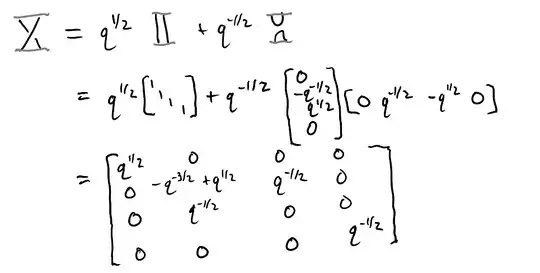
To get the matrices for $B_3$, one can perform the Kronecker product with the $2\times 2$ identity matrix, which has the effect of giving the matrix for a braid with an additional strand on one side. These were checked in Mathematica to satisfy $\sigma_1\sigma_2\sigma_1=\sigma_2\sigma_1\sigma_2$:

\begin{align} \sigma_1 &= \left( \begin{array}{cccccccc} \sqrt{q} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{q} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \sqrt{q}-\frac{1}{q^{3/2}} & 0 & \frac{1}{\sqrt{q}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \sqrt{q}-\frac{1}{q^{3/2}} & 0 & \frac{1}{\sqrt{q}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{q}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{\sqrt{q}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \sqrt{q} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \sqrt{q} \\ \end{array} \right) \\ \sigma_2 &= \left( \begin{array}{cccccccc} \sqrt{q} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{q}-\frac{1}{q^{3/2}} & \frac{1}{\sqrt{q}} & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{q}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \sqrt{q} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \sqrt{q} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \sqrt{q}-\frac{1}{q^{3/2}} & \frac{1}{\sqrt{q}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{\sqrt{q}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \sqrt{q} \\ \end{array} \right) \end{align}

This representation splits into irreducibles for generic values of $q$ (that is, except for a few roots of unity). In particular, this eight-dimensional representation splits as $2V_1\oplus V_3$. The projection onto the $V_3$ summand is given by the third Jones-Wenzl projector, which graphically can be written as

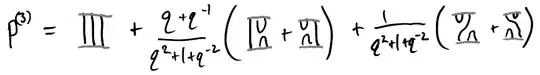
and with some elbow grease this may be turned into an $8\times 8$ projection matrix. (For $q=1$, this is the projection onto $\operatorname{Sym}^3 V_1$.)