4

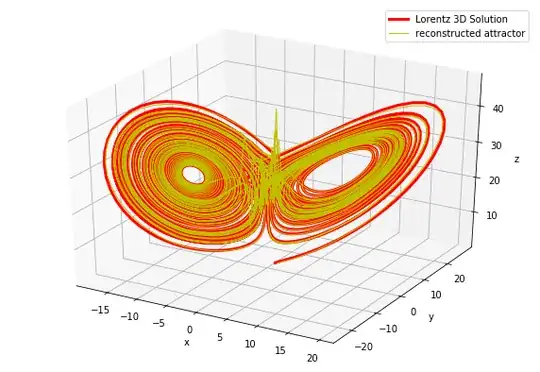
I'm investigating attractor reconstruction of Lorenz system. I saw a bunch of work claiming that the time delay map $[x(t), x(t -\tau), x(t - 2\tau)]$ is sufficient to reconstruct the attracotr, e.g. http://www.scholarpedia.org/article/Attractor_reconstruction, https://www.youtube.com/watch?v=6i57udsPKms.

If I'm understanding this correctly, this means that the state space of Lorenz system can be embedded into $\mathbb{R}^3$. However as far as I have known by Takens' theorem, the time delay step $n$ to embed a strange attractor of dimension $d$ should be $n \geq 2d+1$. In this sense, since the fractal dimension of Lorenz attractor is slightly greater than $2$, there should be at least $5$ delay steps in order to achieve the embedding.

Is there any specific theorem/paper claiming that the Lorenz attractor can be embedded by a 3-step time delay embedding?

mw19930312
  • 315
  • Welcome to Mathematics Stack Exchange! Great post! A quick tour will hep you understand how best to form questions and answers. – dantopa Jan 16 '19 at 21:30
  • The theorem gives a guarantee for $n\ge 2d+1$, but does not claim that smaller $n$ do not work. // The similar image is for $τ=0.1$, just doubling it to $τ=0.2$ gives a much curvier surface. – Lutz Lehmann Jan 16 '19 at 22:26
  • @LutzL Thanks for the reply! I understand that Takens' theorem only provides an upper limit. What I'm concerned is that $[x(t), x(t-\tau), x(t-2\tau)]$ does not seem to be an embedding since I could not find any rigorous theorem says so. Do you happen to now any reference? – mw19930312 Jan 17 '19 at 15:06
  • No, only the argument put forward in the answer that the system is sufficiently coupled that the map from $[x(t),y(t),z(t)]$ to the states at $t−τ$ and $t-2τ$ and then projecting down to $[x(t),x(t−τ),x(t−2τ)]$ is bijective, so that the dynamics is faithfully captured in the 3-step delay map. // When plotting, it helps much for smaller $τ$ to apply a linear transformation and plot the curve [(x(t)+x(t−τ)+x(t−2τ)),(x(t)-x(t−2τ)),(x(t)-2x(t−τ)+x(t−2τ))]$. – Lutz Lehmann Jan 17 '19 at 15:13

2 Answers2

1

this means that the state space of Lorenz system can be embedded into $\mathbb{R}^3$.

Without a restriction to delay embedding, this is trivial since the Lorenz system consists of three differential equations.

However as far as I have known by Takens' theorem, the time-delay step $n$ to embed a strange attractor of dimension $d$ should be $n \geq 2d+1$.

The dimension given by Takens’s theorem is only an upper limit. A lower embedding dimension may suffice. Also see this question and answer.

Also note that Takens’s theorem doesn’t use fractal dimensions at all; it’s the Sauer–Yorke–Casdagli theorem that does.

Is there any specific theorem/paper claiming that the Lorenz attractor can be embedded by a 3-step time delay embedding?

Given that the Lorenz attractor can be embedded in three dimensions (see above), it would be intuitively surprising if a three-dimensional delay embedding fails here (in particular for all delays). Moreover, and maybe most importantly, three-dimensional delay embeddings of the Lorenz attractor have been used extensively investigated for benchmarking, proofs of principle, or similar – which, to my knowledge, hasn’t turned up any inconsistencies as to be expected for a failed embedding.

I am not aware of rigorous investigations of this, but I wouldn’t be surprised if none exist, due to a lack of relevance: The entire point of a Takens embedding is to reconstruct attractors of unknown dynamics. Applying it to something like the Lorenz system is only for benchmarking, proofs of principle, etc.

Wrzlprmft
  • 5,926
  • Thanks for the reply! By saying "Given that the Lorenz attractor can be embedded in three dimensions (see above), it would be surprising if a delay embedding fails here (in particular for all delays).", do you mean that since Lorenz attractor can be embedded into $\mathbb{R}^3$, there must exist time delay embedding with $n\geq 7$? Actually I don't know whether $[x(t), x(t - \tau), x(t - 2\tau)]$ is an embedding since there is no theorem substantiate it. All existing work I've found assume this by default since trajectory of original system looks similar to time-delayed trajectory.... – mw19930312 Jan 17 '19 at 15:11
  • @mw19930312: Please see my edit. – Wrzlprmft Jan 17 '19 at 15:36
1

As to why 3 delay steps are sufficient for the Lorenz system:

We know that by Taylor $$ \frac{x(t+τ)-x(t-τ)}{2τ}=\dot x(t)+\frac{τ^2}6\dddot x(t)+... $$ and $$ \frac{x(t+τ)-2x(t)+x(t-τ)}{τ^2}=\ddot x(t)+\frac{τ^2}{12}x^{(4)}(t)+... $$ Now insert the Lorenz differential equations $$ \left.\begin{aligned} \dot x&=σ(y-x)\\ \ddot x&=σ(x(\rho-z)-y-\dot x) \end{aligned}\right\} \implies \left.\begin{aligned} y&=x+\frac{\dot x}σ\\ z&=\rho-\frac{y+\dot x+\frac{\ddot x}σ}{x} \end{aligned}\right\} $$ to see that up to order $τ^2$ the values of $y(t)$ and $z(t)$ are easy to extract from the difference quotients and the first derivative terms on the right.

enter image description here

Reconstruction using above approximations and $\tau=0.03$. The reconstructed curve follows closely the original curve, except close to $x=0$ where the division-by-zero leads to singularities, even in a mollified division.

Involving higher order derivative terms gives a system of higher degree that will provide a more exact relation between the two sets of data. But even this first approximation shows that it is possible to invoke the inverse function theorem as long as $x\ne0$ to get a bijection.

Lutz Lehmann
  • 131,652