Solve advection equation $v_t + v_x = 1$ numerically with Matlab

Question

Consider the advection equation

$$ v_t + v_x = 1 $$

with initial condition

$$ v(x,0) = \begin{cases} \sin^2 \pi (x-1), & x \in [1,2] \\ 0, & \text{otherwise} \end{cases}$$

Clearly, we know that for any $F$, the general solution is

$$ v(x,t) = F(x - s t) $$ and $v(x,0) = F(x) = \sin^2 \pi (x-1)$. Therefore, the solution we are looking for is

$$ v(x,t) = \sin^2 \pi (x-1-st) $$

where $s$ is constant.

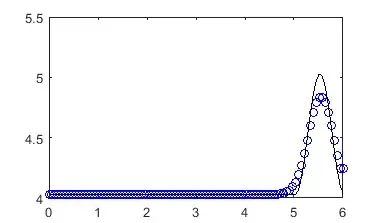
My question is how do we implement the solution numerically in matlab? Numerically, we can discretize the PDE using the following scheme Lax

$$ \frac{ u_j^{n+1} - \frac{1}{2}( u_{j+1}^n + u_{j-1}^n) }{\Delta t} + \frac{ u_{j+1}^n - u_{j-1}^n }{2 \Delta x} =0 $$

say for $x \in [0,6]$ and $t \in [0,4]$

Answer 1

For $v_t+v_x=1$, the solution to the Cauchy problem $v(x,0)=F(x)$ obtained with the method of characteristics is $$ v(x,t) = F(x-t) +t . $$ The Lax-Friedrichs method reads $$ \frac{v_i^{n+1}-\frac{1}{2}(v_{i-1}^{n}+v_{i+1}^{n})}{\Delta t} + \frac{v_{i+1}^{n}-v_{i-1}^{n}}{2 \Delta x} = 1 $$ where $v_i^n \simeq v(i\Delta x, n\Delta t)$. This method is stable for small time steps according to the Courant-Friedrichs-Lewy condition $\Delta t < \Delta x$. Now, we only need to translate the previous algorithm into MATLAB syntax.

%% Initialisation
F = @(x) sin(pi*(x-1)).^2 .* (1<x).*(x<2);

n = 100;
x = linspace(0,6,n);
dx = 6/(n-1);
t = 0;
dt = 0.95*dx;
v = F(x);

figure;
plot(x,v,'k-');

%% Scheme iterations
while t<4
    v(2:n-1) = 0.5*((1+dt/dx)*v(1:n-2) + (1-dt/dx)*v(3:n)) + dt;
    v(1) = v(2);
    v(n) = v(n-1);
    t = t + dt;
end

%% Output
plot(x,v,'bo');
hold on
plot(x,F(x-t)+t,'k-');