5

When trying to identify a limit cycle of a 2nd order nonlinear DE $$\begin{cases}\dot{y}_1=y_2\\\dot{y}_2=-ky_2-\frac{b(a)sin(y_1)}{1+c_1(a)cos(y_1)+c_2(a)sin(y_1)}\end{cases},$$ where $b(a)$, $c_1(a)$, and $c_2(a)$ are some coefficients depending on the parameter $a$, I arrived at the following 1st order PDE: $$\frac{\partial V}{\partial y_1}y_2-\frac{\partial V}{\partial y_2}ky_2-\frac{\partial V}{\partial y_2}f(y_1)=0.$$ I wish to find a solution to this equation in the form $V(y_1,y_2)=0$ such that the following conditions are satisfied:

  1. $V(y_1+2\pi,y_2)=V(y_1,y_2)$;
  2. $\frac{dy_2}{dy_1}\bigg|_{y_1=0}=0$ and $\frac{d^2y_2}{dy_1^2}\bigg|_{y_1=0}>0$;
  3. $\frac{dy_2}{dy_1}\bigg|_{y_1=\pi}=0$ and $\frac{d^2y_2}{dy_1^2}\bigg|_{y_1=\pi}<0$.

Item 1 comes from the fact that the DE is defined on a cylinder, while Items 2 and 3 say that the plot $y_2=y_2(y_1)$ of $V(y_1,y_2)=0$ has a minimum at $y_1=0$ and a maximum at $y_1=\pi$. The latter conditions were obtained from numerical simulations.

Furthermore, we know that $f(y_1+2\pi)=f(y_1)$ and $f(0)=0$.

Question: I wonder whether this problem is well defined and if "yes", how to solve it?

Indeed, I want to find the limit set $V(y_1,y_2)=0$ since the problem -- as it is stated -- can have only one solution that corresponds to the limit cycle.

My attempts. Let $y_1=0$. If $\frac{\partial V}{\partial y_2}\bigg|_{y_1=0}\neq 0$, Item 2 along with $f(0)=0$ implies that $y_2=0$ which contradicts the fact that the point $(0,0)$ is an isolated equilibrium. So, I conclude that $$\frac{\partial V}{\partial y_2}\bigg|_{y_1=0}= 0 \mbox{ and } \frac{\partial V}{\partial y_1}\bigg|_{y_1=0}= 0.$$ Following the same logic I conclude that the same holds for $y_1=\pi$: $$\frac{\partial V}{\partial y_2}\bigg|_{y_1=\pi}= 0 \mbox{ and } \frac{\partial V}{\partial y_1}\bigg|_{y_1=\pi}= 0.$$

So, basically, that's it. I tried several candidates for $V(y_1,y_2)$, but couldn't get any meaningful result.

This plot makes me to believe that there is a limit cycle. The red trajectory (approximately) corresponds to the unstable solution of the sadle, two others are just computed for different initial values of $y_2$. enter image description here

Dmitry
  • 1,347
  • Could you also write down the ODE? Also, it seems that you don't really want a function $V$ but just the level set $V = 0$. Please clarify this! – Hans Engler Jan 10 '19 at 13:44
  • Dear @Hans, I added the DE and commented about what I'm after. Indeed, I want to determine the level set which corresponds to the invariant (= limit cycle) of the DE. – Dmitry Jan 10 '19 at 14:06
  • 2
    Isn't it an overkill to switch to PDE here? You can safely assume that a limit cycle is a graph $y_2 = F(y_1)$, where $F(0) = F(2\pi k)$, and use Fourier series after that. Quite similar to what you have done previously for finding saddle's separatrix in this system. – Evgeny Jan 10 '19 at 22:16
  • Dear @Evgeny, this is a fair point. I'll definitely do as you suggested. I turned to PDEs as I wanted to explore different options. Also, the PDE seemed quite simple to me so I hoped to get some more information beyond what I get with series expansion. – Dmitry Jan 11 '19 at 08:14
  • 2
    I recall that PDEs were used by Sacker as an alternative method for proving existence of limit cycles or invariant tori in Andronov-Hopf and Neimark-Sacker bifurcations. You can take a look at this method here. The PDE he used was quite similar to yours, however it seem that he slightly modified PDE for the sake of easier control of solution behaviour. – Evgeny Jan 11 '19 at 09:15
  • 1
    I also want to comment on item 2 of your boundary conditions. Geometrically it has to agree with how trajectories start on $y_1 = 0$. If you check vector field at $(0, y_2)$ it is $(y_2, -k y_2)$. Your condition 2 means that tangent vector to a solution is $(\text{}, 0)$, but there is no point with such vector on this line. There could be a periodic solution to this equation, but not with this boundary condition. – Evgeny Jan 11 '19 at 11:35
  • @Evgeny, you are right. I overlooked that. In fact, the minimum (and the maximum) are slightly shifted away from $0$ ($\pi$). This makes the problem even more difficult... I'll get back to the problem on Monday and report about my advances. – Dmitry Jan 12 '19 at 17:03
  • 2
    By the way, I might be quite wrong here, but do you really expect a limit cycle here? Take the "unperturbed" system when $k=0$: in that case system has a first integral. Do you know what is the level set structure of this system? This first integral would be a Lyapunov function (sort of) when $k$ is small; see the illustration here and explanation here, for example. ... – Evgeny Jan 12 '19 at 17:33
  • 1
    ... So there is a possibility for having no limit cycles here. – Evgeny Jan 12 '19 at 17:34
  • @Evgeny, thank you for the advice. I've read your previous posts and these are very helpful and instructuve indeed. However, I didn't manage to advance any further. 1) I posted a picture of numerical simulation that looks very much after a limit cycle. Unfortunately, I do not know how to plot on a cylinder. Prehaps this would be more illustrative. 2) I tried to find an analytic expression for the integrals in the undamped case ($k=0$), but the expressions are too complex to be useful. 3) finally, I computed a Fourier approximation of a periodic solution, but differs pretty much from what – Dmitry Jan 16 '19 at 10:23
  • ... I see in numerical simulation. Perhaps the problem is that I consider very truncated series (up to $\sin(3y_1)/\cos(3y_1)$), but when I increase the order, my Matlab fails to deliver any solution to the system of equations defining the coefficients. So,... I will continue attacking this problem and get back when I obtain any new results. Many thanks for your help once again. – Dmitry Jan 16 '19 at 10:27
  • You are welcome! What you are observing here is pretty interesting. "The energy" $$\frac{y^2_2}{2} + \int \frac{b(a)\sin(y_1)}{1+c_1(a)\cos(y_1)+c_2(a)\sin(y_1)} , dy_1$$ must decrease in time since its time derivative is just $-ky^2_2$. However, if level sets of $$\frac{y^2_2}{2} + \int \frac{b(a)\sin(y_1)}{1+c_1(a)\cos(y_1)+c_2(a)\sin(y_1)} , dy_1$$ are quite intricate, maybe a rotational limit cycle can happen. Can you please tell particular values of $k$, $c_1(a)$, $c_2(a)$ and $b(a)$ that you've used to plot the last graph? – Evgeny Jan 16 '19 at 13:03
  • Sure! Here is the model (copied from my Matlab with little formatting): $\dot{y}_1=y_2$; $\dot{y}_2=-\kappay_2-\beta(\sin(y_1-a)+\sin(y_1+a))/((\tau+1)\psi+\tau\cos(y_1-a)+\cos(y_1+a))$, where $\kappa = 0.2$, $\beta = 150$, $\psi = 1.3$, $\tau = 0.8$, $a=3.9/2$. It slightly differs from the model written above, but can be transformed to it. I copy it here as is to avoid possibly typos. – Dmitry Jan 16 '19 at 13:16
  • 1
    Well, at least now I know the key difference between your unperturbed system and mathematical oscillator. The first integral of mathematical oscillator is defined on cylinder as the system itself whereas the first integral of your system is not periodic in $y_1$ and is a function only on a plane, not a cylinder. If the first integral of unperturbed system was also defined on a cylinder (i.e, were periodic in $y_1$), limit cycles would be ruled out in perturbed system, but now there is still room for them. – Evgeny Jan 17 '19 at 08:36
  • @Evgeny, that is a very interesting observation! Could you expand on that a bit or give a reference? Thanks! – Dmitry Jan 17 '19 at 09:12
  • 1
    Basically, you have a function $\mathcal{F}$ that is non-increasing along trajectories (I've described it few comments before). Such function often rules out closed trajectories: suppose the system has closed trajectory $\gamma(t)$, after the period you return back to the same point, but $\mathcal{F}$ has to decrease along the trajectory and you have contradiction: $\mathcal{F}(\gamma(0)) = \mathcal{F}(\gamma(T)) < \mathcal{F}(\gamma(0))$. But if you have a system on cylinder, there is another kind of closed trajectory: e.g., you start at $(-\pi, z)$ and after period come to $(\pi, z)$. ... – Evgeny Jan 17 '19 at 10:14
  • ... These are different points on the plane, and no contradiction waits readily here unless $\mathcal{F}(-\pi, z) = \mathcal{F}(\pi, z)$. This happens when $\mathcal{F}$ is periodic in the first coordinate. However, $\mathcal{F}$ that comes from your unperturbed system is not periodic in the first coordinate, as far as I've computed. ... – Evgeny Jan 17 '19 at 10:26
  • ... There is still one way how your $\mathcal{F}$ can rule out closed trajectories. Consider a level set of $\mathcal{F}$ that passes through $(-\pi, z)$ and consider its intersection with $y_1 = \pi$ (let it be at $(+\pi, z^\ast)$. If $z^\ast < z$ you can't have a 'closed' trajectory that starts at $(-\pi, z)$ and lands at $(+\pi, z)$. The reasoning behind this is that a trajectory of perturbed system would land on the point with even lower second coordinate than $z^{\ast}$. I'm still taking a look at this with numerics. – Evgeny Jan 17 '19 at 10:33

2 Answers2

3

Let me summarize here some ideas from comments and one weird finding of mine. This is not a complete answer, but I think I have found some explanation for what's happening.

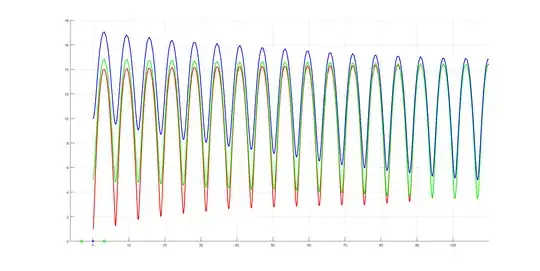
As @Dmitry told, numerics show that system has a rotational limit cycle. Standard ways to prove existence of limit cycle for some parameter values include understanding what bifurcation could give rise to this limit cycle. To get a grasp on which bifurcation exactly happens it is reasonable to vary parameters and see what happens. Changing $k$ is a good idea: when $k=0$ the system is particularly simple and some analytics could be done. Naturally I was trying to understand what happens with limit cycle when you decrease $k$ to $0$. This is important because when $k = 0$ no such limit cycle is possible, I'll explain why further. The weird finding is that the more I decrease $k$ to $0$, the higher and higher this rotational limit cycle goes. That's weird and slightly suggests that bifurcation happens at infinity when $k = 0$. I am not good at dealing with bifurcations at infinity, for me it looks like some sort of weird "Andronov-Hopf at infinity", but I've never met myself such bifurcation before.

I think the picture is a bit more tractable when you start increasing $k$: at some value close to $k = 0.215$ it seems that rotational limit cycle collides with a heteroclinic trajectory connecting two saddles. It would be a good idea to figure out how stable separatrices of saddles behave before and after this bifurcation: they are always part of boundaries between different attraction basins and can help figure out multistability. You know about stable focus in this system (which is unique on the cylinder), thus the presence of another attractor might mean that a limit cycle exists.

Here I'll try to explain why rotational closed trajectories exist when $k \approx 0$. I'll start with "unperturbed" version of OP's equations, i.e. when $k = 0$. In that case system takes a form $\dot{x} = y, \, \dot{y} = -f(x)$. If you consider an equation $$\ddot{x} + f(x) = 0,$$ where $f(x)$ is at least continuous, it is well know that all such equations are integrable: the first integral is simply $\frac{\dot{x}^2}{2} + F(x)$, where $F(x)$ is such that $F'(x) \equiv f(x)$. If $f(x)$ is periodic, then we can consider an equivalent system $$ \dot{x} = y, $$ $$ \dot{y} = -f(x),$$ which is naturally a system on a cylinder. As a system on plane it also has a first integral which is $\frac{y^2}{2} + F(x)$. Note that $F(x)$ might be not periodic and hence the system on cylinder wouldn't have a first integral. Using the system on the plane and the first integral we can compute Poincaré map for $x = 0$ and $x = 2 \pi$ as cross-sections. Namely, $$ \frac{\lbrack y(0) \rbrack^2}{2} + F(0) = \frac{\lbrack \overline{y} \rbrack^2}{2} + F(2\pi),$$ or $$ \overline{y} = \sqrt{y^2 - 2(F(2\pi)-F(0))}$$ if we start with $y > 0$.

For the parameter values that @Dmitry mentioned in comments $F(2\pi) - F(0)$ is negative and doesn't depend on $k$. So I'll just write map as $\overline{y} = \sqrt{y^2 + \alpha}$, where $\alpha > 0$. Any rotational closed trajectory would correspond to a fixed point of this Poincaré map, i.e. to a solution of $y = \sqrt{y^2 + \alpha}$. It is quite obvious that there is no solution to this equation because $\sqrt{y^2 + \alpha} > \sqrt{y^2} = y$. However what happens, if we perturb this mapping a bit? For example, does $\beta + \sqrt{y^2 + \alpha} = y$ has solutions for $\beta \approx 0$? The answer is "no" when $\beta > 0$, but when $\beta < 0$ the answer is "yes". The function $\beta + \sqrt{y^2 + \alpha}$ has line $y + \beta$ as an asymptote, thus $(\beta + \sqrt{y^2 + \alpha}) - (\beta + y)$ tends to $0$ as $y \rightarrow +\infty$. From this follows that $\beta+\sqrt{y^2 + \alpha} - y \rightarrow \beta$, thus it is negative at some values of $y$, but positive when $y = 0$ it is positive. An existence of fixed point follows from continuity. Note that this fixed point ceases to exist when $\beta = 0$, but it exists for small $\beta < 0$: smaller $\beta$ corresponds to bigger coordinate of fixed point, "it comes from infinity".

My idea is that although the real perturbation of Poincaré map would be much different than my model example, something quite similar happens when $k$ is non-zero in your system. Probably it could be made more rigorous, but I didn't delve much into it.

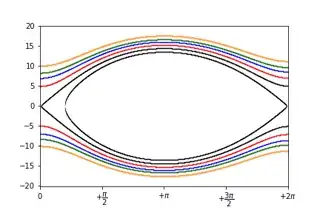
This is an illustration of level sets for $\frac{y^2}{2} + F(x)$. Black level sets contain saddle equilibria. $F(x)$ was evaluated numerically using quad function from SciPy. Level sets

Note that the point at which level set intersects $x = 0$ is lower than the point of intersection with $x = 2\pi$. It happens due to aperiodicity of $F(x)$; in particular, $F(2\pi) - F(0) < 0$.

Evgeny
  • 5,895
  • sorry, was not able to check math.SE for a couple of days. Will digest and comment on your answer within the next two days. Many thanks for putting so much effort into it. – Dmitry Jan 23 '19 at 15:25
  • No problem, feel free to ask as many questions as you need, some moments might have been outlined not ideally. It's an interesting problem, I've enjoyed thinking about it. Is this a part of your Masters or PhD thesis? – Evgeny Jan 23 '19 at 17:22
  • Many thanks, your observation is very useful. I'll add a couple of questions in the next comment. Regarding the problem: it is a simplified model of a technical system that I study with a colleague of mine. I can give you more details if you are interested. Any help/participation is very welcome. I'm actually already done with my PhD and currently do research in control with applications. – Dmitry Jan 25 '19 at 12:03
  • There are two questions: 1) why do you call this bifurcation a sort of Andronov-Hopf? This seems to be a global bifurcation while the A.-H. is a local one. 2) How is it possible to have limit cycle s.t. $F(2\pi)<F(0)$. This inequality would imply that the potential function decreases along the trajectories even without damping. – Dmitry Jan 25 '19 at 12:08
  • 1
  • Sorry for confusing this with a part of PhD/Master thesis: I haven't seen many actual research problems appearing on MSE, hence my ignorance :) 1) This is a kind of analogy, but I imagine it like that. I think you know about compactifying a plane by gluing one point and getting a sphere? Let's compactify our cylinder by gluing two points: one to the top and another to the bottom. This will give two new stable equilibria when $k = 0$. But if we take $k \neq 0$ we instantly have a limit cycle that "comes from infinity". Hence my analogy that equilibrium at infinity went Andronov-Hopf.
    • – Evgeny Jan 25 '19 at 16:54
  • I was educated as an engineer, hence my math-background is pretty patchy. Sometimes I use MSE to close the gaps in my education (referring to google scholar: "to climb up the shoulders of giants" :). 1) got it, thanks.
    • – Dmitry Jan 25 '19 at 17:38
  • 1
  • I've added to the answer an illustration for level sets of first integral when $k=0$. I don't know how reasonable this is from physics point of view, but you are right, potential energy decreases, but this loss is compensated by increasing the velocity.
    • – Evgeny Jan 25 '19 at 17:48