3

I needed to find: $$\lim\limits_{x\to +\infty}(x-\ln(x^2+1))$$

So here are the steps I took:

Step 1: Replace $x$ with $\ln(e^x)$: $$\lim\limits_{x\to +\infty}\left(\ln(e^x)-\ln(x^2+1)\right)$$ $$\lim\limits_{x\to +\infty}\ln\left(\frac{e^x}{x^2+1}\right)$$

Step 2: Bring the limit inside of the natural log function since it is continuous on the required interval.

$$\ln\left(\lim_{x\to +\infty}\frac{e^x}{x^2+1}\right)$$

Step 3: Apply L'Hospital's rule twice and evaluate:

$$\ln\left(\lim_{x\to +\infty}e^x\right)$$

$$\ln(+\infty) = +\infty$$

My question is whether step 2 is valid here because $\lim\limits_{x\to \infty}\frac{e^x}{x^2 + 1}$ doesn't exist (its $+\infty$), and in order to move the limit operator inside the function the limit $\lim\limits_{x\to \infty}\frac{e^x}{x^2 + 1}$ must exist according to this theorem in a book about Calculus (ISBN 978-0-470-64769-1):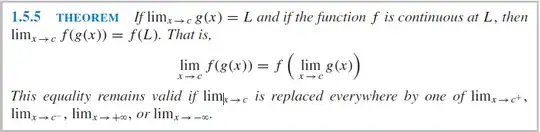enter image description here

If it's not valid, what would be a valid way to find the limit?

rtybase
  • 17,398
Stefan Dimeski
  • 297
  • 1
    Your step is valid. The book deals with the theorem where the limit does exist. Similar result holds if the limit does not exist. See the theorem mentioned at the end of this answer: https://math.stackexchange.com/a/1073047/72031 – Paramanand Singh Jan 06 '19 at 02:24

2 Answers2

1

Let $M>0$ be given. Since $\ln(u)\to \infty$ as $u\to\infty$, there exists $K$ such that for all $x$ with $\frac{e^x}{x^2+1}>K$ it follows that $\ln\left(\frac{e^x}{x^2+1}\right)>M$. Since $\frac{e^x}{x^2+1}\to \infty$ as $x\to \infty$, there exists $N$ such that $$ x>N\implies \frac{e^x}{x^2+1}>K\implies \ln\left(\frac{e^x}{x^2+1}\right)>M. $$
By definition of a limit it follows that $$ \lim_{x\to\infty}\frac{e^x}{x^2+1}=\infty. $$

Note we can mimic the same argument to conclude that if $f(x)\to \infty$ as $x\to \infty$ and $g(x)\to \infty$ as $x\to \infty$, then $g(f(x))\to \infty$ as $x\to \infty$.

Sri-Amirthan Theivendran
  • 31,832
  • That's a nice clean way, thanks! Can you please explicitly answer the first question: whether the way I did it is mathematically valid or invalid? – Stefan Dimeski Jan 06 '19 at 00:19
1

In step 2 all you need is the fact that $\ln (y) \to \infty$ as $y\to \infty$. Since $\frac {e^{x}} {x^{2}+1} \to \infty$ it follows that $\ln (\frac {e^{x}} {x^{2}+1}) \to \infty$. To prove that $\ln (y) \to \infty$ as $y\to \infty$ assume that this is false. Since $\ln \, x$is an increasing function, if it doesn't not tend to infinity, it would be bounded for $x>1$, say $\ln\, x <C$ for all $x>1$. You get a contradiction from this if you take $x=e^{C}$.

Kavi Rama Murthy
  • 359,332