0

I'm really in trouble trying to understand Itô integral. I can work with it without any problem, but I don't understand what is it. And why is it an integral? How can we interpret $$I=\int_0^T f(s,B_s)dB_s \ \ ?$$

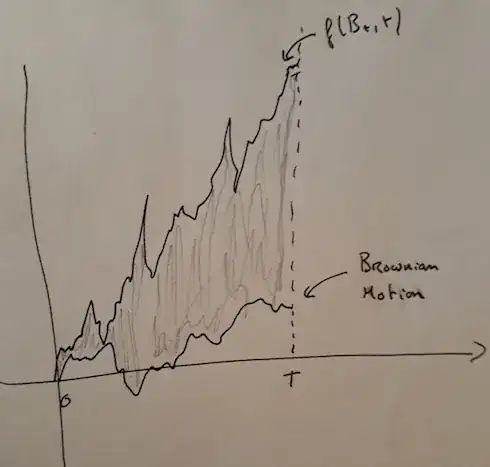
  • Would it be: we consider the Brownian Motion on $[0,T]$ and a function $f:[0,\infty )\times \mathbb R\to \mathbb R$, then the area between $(B_t)_{t\in [0,T]}$ and $(f(t,B_t))_{t\in [0,T]}$ is a sort of Itô integral $I$? (in grey in the following picture)

enter image description here

  • Why are we interested in this integral? I also saw that if $H_s$ is the number of call we have then $\int_0^T H_s dB_t$ is the profit we made after $[0,T]$. If so, why the price of a call is a Brownian Motion? This is very weird for me.
FD_bfa
  • 4,757
user623855
  • 465
  • 1
    The stochastic integral doesn't represent an area as a Riemann integral. The stochastic integral is just a stochastic process that has the same properties than the integral, that's why we use the integral notation. – Surb Dec 29 '18 at 11:09
  • Your first suggestion is bizarre since usual integrals are never this area... – Did Dec 29 '18 at 11:10
  • @Did : I add a picture to be more clear. Maybe something in this spirit ? (probably not exactely that, but is to relate this to an area). I'm trying to make a comparaison with stiljes integral, but maybe such integral can't be related to an area, doest it ? – user623855 Dec 29 '18 at 11:18
  • @Surb : And for the interpretation ? – user623855 Dec 29 '18 at 11:18
  • But already for $f(B_t,t)=1$, this interpretation fails, as surely you can see... – Did Dec 29 '18 at 11:19
  • @Did : Indeed, so what is the interpretation of the stochastic integral ? What is it for you for example ? – user623855 Dec 29 '18 at 11:21
  • An extension of the Stieltjes integral $$\int_0^tf(s)dg(s)$$ to functions $g$ not regular enough for the usual definition to apply. – Did Dec 29 '18 at 11:28
  • @Did: and can such an integral (i.e. stiljes) be seen as an area of something ? – user623855 Dec 29 '18 at 12:02
  • Except when $g$ is monotonous, not really. – Did Dec 29 '18 at 19:45

0 Answers0