2

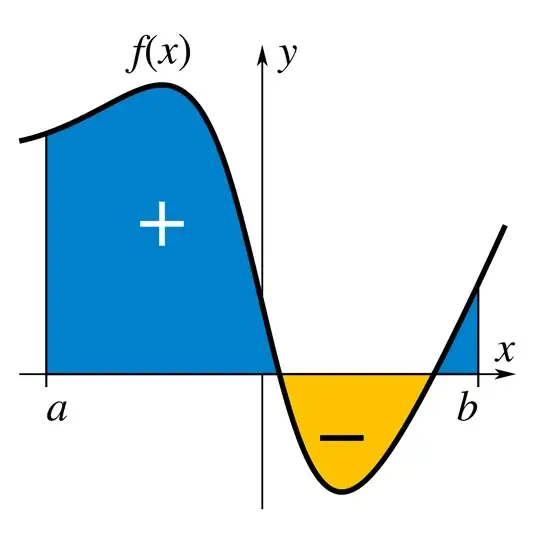
I was told that an antiderivative doesn't represent any area, it is just a family of functions, but today I noticed something quite interesting thing:

If we have $f(x)=2x$, then $F(x)=x^2+C$. The area under $f(x)$ from $0$ to $1$ is $1$, and $F(1)$ is one, the area under $f(x)$ from $0$ to $2$ is $4$, and $F(2)$ is $4$, and so on.

Then I started to think, that when $C=0$, $F(x)$ is the area under $f(x)$ from $0$ to $x$, and tried some others functions like $f(x)=x^2$, $x^3$, and so on.

Then I decided to try $f(x)=\sin x$, and I failed in my guess. But then noticed, if I take $C=1$ it works! Finally, I noticed that it works in all cases when $F(0)=f(0)=0$.

So antiderivative is not only a bunch of functions but also some area?

How can I visualize it generally? How can I visualize $C$? Can this area be an endless area in both directions?

Now I study the fundamental theorem of calculus, and at first, I imagined $F(b)-F(a)$ as $(\text{area from } -\infty \text{ or } 0 \text{ to } b)-(\text{ area from }-\infty \text{ or } 0 \text{ to } a)$. Is it the right visualization?

I will be very grateful if someone could clarify my guesses. Thanks in advance

Upd: thank you all who helped me to solve my problem, i appreciate it so! To one, who faced the same question: there`s a quite similar question, and some of answers are pretty meaningful, for example, this one: https://math.stackexchange.com/a/2559329/595919

Max Knyazeff
  • 23
  • "I was told that an antiderivative doesn't represent any area": don't trust them. –  Dec 18 '18 at 17:58
  • So it does represent some area? – Max Knyazeff Dec 18 '18 at 18:00
  • This is well-known. –  Dec 18 '18 at 18:03
  • So could u tell me please what area does it represent? – Max Knyazeff Dec 18 '18 at 18:05
  • As usual, between the axis, curve and verticals. –  Dec 18 '18 at 18:09
  • If the antiderivative represents a family of functions, indexed by C, then you could say it represents a family of area calculations, each indexed by C. In your first example you fixed C by fixing the first integral [0, 1] then comparing all others to that. For the sin(x) example, you should be able to find an arbitrary C that depends on [a, b] and compare all areas to that. –  Dec 18 '18 at 19:44
  • The antiderivative (also known as an indefinite integral) is a family of functions. But you can use it to compute “area under the curve,” especially by converting it into a definite integral. – David K Dec 19 '18 at 15:56

2 Answers2

0

Firstly, you can visualize an anti-derivative as a curve itself, whose derivative yields the function with which you are concerned. This new curve can be translated up and down without affecting the slope, therefore you can visualize C as an ambiguous translation of that curve up and down.

As for your understanding of the Fundamental Theorem of Calculus, I would not interpret it as two areas, but rather as the area between a and b itself, which can be found using your anti-derivative function.

I hope that helps.

RJJB
  • 13
0

Let $f\colon \Bbb R\to\Bbb R$ be a function that has an anti-derivative $F$. Let $a<b$ be real numbers, then you can use $F$ to calculate the (oriented) area between the vertical lines $x=a$ and $x=b$ that sits between the $x$-axis and the graph of $f$:

oriented area

More precisely we have $$ \color{blue}{\text{blue area}} - \color{orange}{\text{orange area}} = \int_a^b f(x)\,\mathrm dx = F(b) - F(a). $$

Note that the choice of constant in the anti-derivative doesn't matter here, since it cancels when calculating the difference $F(b)-F(a)$.

Letting $a=0$ and choosing the constant such that $F(0)=0$ you get that $F(a)$ is the area under the curve between $x=0$ and $x=a$, as you figured out.

Christoph
  • 25,552