Slant cone volume problem

Question

I was given a a problem to solve, I thought I solved it but my answers don't look like the ones provided.

The Problem

A cone with radius of base r and height h, is stretched to the left and right by length a and b respectively such that height of the stretched cones equals to the height of the original cone and apexes of all the three cones are colinear.

Devise an algorithm to calculate the volume of the union of the two stretched cones (colored blue in the image).

My first question was: what is the volume of a slant cone? What I've found so far is that the formula for the volume of a slant cone is the same as that of a regular cone (which made sense to me).

So I though the answer would be 2 times the area of a cone given by radius r and height h minus the intersection of the two slant cones, which is also a cone with radius r. I just need to find out the height of that smaller cone.

My thought was that I could just take the cross section of of the bodies and handle the problem in 2D. Where the base of the cone will lie on the x axis and the center for the circle lies in point (0,0).

What I did was calculate the equation of the line that goes from (-a,h) to (r,0). And I would also calculate the equation of the line going from (-r,0) to (b,h).

I proceeded to calculate the line equations and then to calculate where they intersect. I would then take y value at intersection and use it as the height of the smaller cone.

I really thought I nailed it since when I had a = 0 and b = 0 I got the volume of the original cone. However, when the answers where provided mine didn't match the ones given. Can someone point out the hole in my logic?

I' not convinced (just at very first glance) that the intersection be a cone as well .. how do you reached at that? — G Cab, Dec 18 '18 at 00:00
@GCab I didn't prove it, which might me the problem in my attempt at reaching the solution. I just thought it natural, because if the ratio of the slopes is -1, I get an isosceles triangle, which, can then be turned into a cone by revolving around the y-axis. — Nerdrigo, Dec 18 '18 at 00:16
so long as the height of the cone remains constant, volume does not change. The volume of an oblique cone is still the same as the non-oblique version.
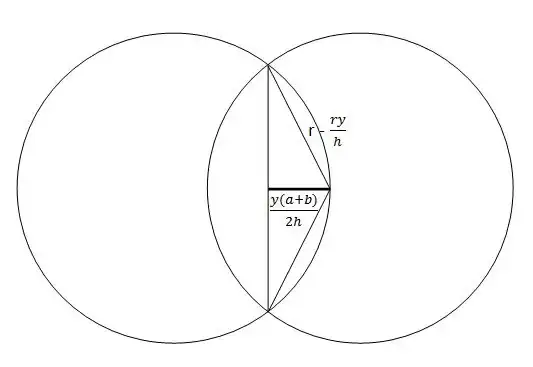
Think of the version with a right triangle. The area is always base times height, we don't care how stretched out it is so long as we know this data. — DaveNine, Dec 18 '18 at 00:26

G Cab · Accepted Answer · 2018-12-18T10:15:42.143

2

For the principles of projection onto parallel planes, on a plane $z=c$, the section of the three cones are circles of same radius $r(h-c)/h$, and centers shifted in the same ratio $c/h$ wrt $a,b$.

So the intersection is a " conic wedge" structure: the superposition of the intersections of the shifted circles.

Then by Cavalieri principle, you can slant the cones symmetrically by $(a+b)/2$ wrt the right cone, compute the intersection of the two circles $\cdot dz$, and integrate.

edited Dec 18 '18 at 10:15

answered Dec 18 '18 at 00:59

G Cab

35,964

I think is a cone, but needs to be is like a cone, but —since the intersection of the circles isn't circular. (I spent a while trying to convince myself that the intersection somehow did manage to be conical.) – timtfj Dec 18 '18 at 01:20
@timtfj Correct, the intersection is a series of increasing radius (downwards) intersecting circles where they completely overlap each other at the base. – Phil H Dec 18 '18 at 02:15

score 1 · Answer 2 · answered Dec 18 '18 at 21:18

The volume of the intersection is given by the following integral based on a general equation for the area of the intersection of two same-sized circles in this scenario, dependent on the value of y:

$$V_i =\int_0^{h_i}\big(2\cos^{-1}(\frac{y(a+b)}{2r(h-y)})\cdot(r-\frac{ry}{h})^2 - \sqrt{(r-\frac{ry}{h})^2-(\frac{y(a+b)}{2h})^2}\cdot(\frac{y(a+b)}{h})\bigr) dy$$

Example: $a=3, b=4, h=5\ \text{and}\ r=3$

$h_i = \frac{30}{13}$ which is the height of the conic wedge

$$V_i =\int_0^{30/13} 2\cos^{-1}(\frac{7y}{6(5-y)})\cdot(3-\frac{3y}{5})^2 - \sqrt{(3-\frac{3y}{5})^2-(\frac{7y}{10})^2}\cdot(\frac{7y}{5}) dy$$

An integral solver couldn't come up with an anti-derivative but used an approximation method and came up with $25.25762\ \#^3$

Slant cone volume problem

2 Answers2