Graph of the composition of a continuous function and a correspondence with a graph homeomorphic to its domain

Question

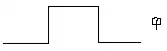
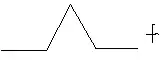
Let $\phi: \mathbb{R}^m \leadsto \mathbb{R}^n $ be an upper hemi-continuous correspondence, $f: \mathbb{R}^n \to \mathbb{R}^n$ be a continuous function. If the graph of $\phi$, $\{(x,y) \in \mathbb{R}^{m+n} \mid y \in \phi(x) \}$, is homeomorphic to its domain $\mathbb{R}^m$. Is it necessarily the case that the graph of $f \circ \phi$, $\{(x,z) \in \mathbb{R}^{m+n} \mid z \in \{f(y) \mid y \in \phi(x)\} \}$, is homeomorphic to its domain $\mathbb{R}^m$ as well?

It is well-known that a continuous function has a graph which is homeomorphic to its domain. So my intuition is that the composition of a continuous function and a correspondence with a graph homeomorphic to its domain make it "closer" to a continuous function ($\#f(\phi(x)) \leq \#\phi(x)$ for all $x \in \mathbb{R}^m$). In this regard, the "worst case" is when $f$ itself is a homeomorphism from $\mathbb{R}^n$ to $\mathbb{R}^n$, and the induced homeomophism is obvious. But is it true in general?

Answer 1

I am new to these definitions so perhaps I am making a dumb mistake, but I believe this is false. I'll try to construct a counterexample.

Let $\phi : \mathbb{R} \rightsquigarrow \mathbb{R}$ be the correspondence given by $$ \phi(x) = \begin{cases} 0 & x < 0 \text{ or } x > 1 \\ [0,1] & x = 0 \text{ or } x = 1 \\ 1 & 0 < x < 1 \end{cases} $$ The graph of $\phi$ looks like a "square bump" of height $1$ on the interval $[0,1]$ and is certainly homeomorphic to $\mathbb{R}$. This is upper hemicontinous if I am understanding definitions correctly. Here's a rough picture:

Let $f$ be the continuous function $$ f(x) = \begin{cases} 0 & x < 0 \text{ or } x \geq 1 \\ 2x & 0 \leq x < 1/2 \\ 2 - 2x & 1/2 \leq x < 1 \end{cases} $$ The graph of $f$ looks like a triangular bump of height $1$ on the interval $[0,1]$. Again a rough picture:

Over the intervals $(\infty, 0), (0,1)$, and $(1, \infty)$ the correspondence $\phi$ is single-valued, so the composition $f\circ \phi$ is as well, and takes the value $0$ identically.

Over the points $x = 0, x = 1$, we have $\phi(x) = [0,1]$, and so we get $$ \lbrace z : z = f(y) \text{ for some } y \in \phi(x)\rbrace = [0,1]. $$

The graph of $f \circ \phi$ (in the $(x,z)$-plane) thus looks like the union of the line $z = 0$ with the sets $\lbrace 0 \rbrace \times [0,1]$ and $\lbrace 1 \rbrace \times [0,1]$, which is not homeomorphic to $\mathbb{R}$. A third picture: