3

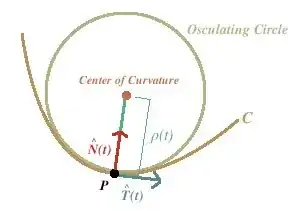
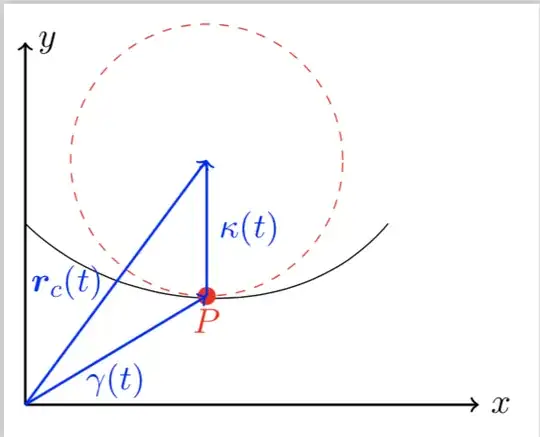
I have found an incongruity into the evaluation of the osculating circle radius of the curve $\gamma(t) = R(cos(t),sin(t))$ using the formula:

$$\vec r_c(t) = \vec \gamma(t) + \vec k(t)$$

Where:

  1. $\vec r_c(t)$ is the vector that identifies the osculating circle centre;
  2. $\vec \gamma(t)$ represents the point $P$ in the picture below;
  3. $\vec k(t)$ is the vector curvature.

Now the problem comes: Rewriting the formula as: $$\vec r_c(t) - \vec \gamma(t) = \vec k(t)$$ and looking the vectors' norm... $$|\vec r_c(t) - \vec \gamma(t)| = |\vec k(t)|$$ I obtain that $R = \frac{1}{R}$ and that's absurd! Can somebody help me to find the mistake?

enter image description here

user515933
  • 573
  • Can you show us how did you conclude $R = 1 / R$? – caverac Nov 30 '18 at 18:19
  • Yes you're right, I should have written the curve that I was considering. Despite that particular case, I can't find anywhere how to obtain the formula $\rho(t) = \frac{1}{|\vec k(t)|}$ using this equality $\vec r_c(t) = \gamma(t) + \vec k(t) $. Because every text I found conseders the formula $\rho(t) = \frac{1}{|\vec k(t)|}$ as a definition of osculating circle radius. – user515933 Nov 30 '18 at 19:29
  • The original formula is wrong. You should be adding the vector $\dfrac1{\kappa(t)} \vec N(t)$ rather than $\vec k(t)$ (which I presume is $\kappa(t)\vec N(t)$). – Ted Shifrin Nov 30 '18 at 20:05
  • I presume you've misunderstood something: take $r(t)=(t-\cos(t),t-\sin(t))$ and $R=1$ and see what happens ... – Michael Hoppe Nov 30 '18 at 20:45
  • But if I consider the curve parametrizaded in arc lenght, the derivate of the tangent vector to a point $\gamma(s)$ of the curve, in other words, $\tau'(s) = \vec k(s)$, is the vector directed to the centre of the osculating circle. Adding to its norm is equal to the radius of the osculating point. But the norm of the vector $\vec k(s)$ is the curvature at the point $\gamma(s)$. But problably I have misundestood the meaning of curvature. So could somebody suggest me a good book to study again this topic? – user515933 Nov 30 '18 at 21:01

1 Answers1

1

The problem starts with your interpretation of the vector ${\kappa}(t)$, according to your first equation, this is what you have

enter image description here

Thats is, the magnitude of $\kappa(t)$ should give you the curvature radius. But that is not the case. I suggest to read this link, it has a good description of the quantities involved

caverac
  • 19,783
  • What I've not undestood yet is the geometrical meaning of the vector $\vec k(t)$. I mean it's the derivate of the tangent vector at the point $P$ of the curve and it's also the vector that links the point $P$ of the curve and the centre of the osculating circle. Furthermore its norm is equal to the value of osculating circle radius. But if my thoughts are right there are some mistakes that I don't undestand. (I've already read the wiki page of the osculating circle but it hasn't clarified me yet) – user515933 Nov 30 '18 at 21:12