How do i find the domain of definition for $u_x + uu_y = 1$ with $u = x/2$ on $y=x$ , $0 \leq x \leq 1$
I parametrise by letting $y=s$ , $x=s$ , $u=s/2$ , $0 \leq s \leq 1$ at $t=0$
The characteristic equations are: $dx/dt = 1$, $dy/dt = u$, $du/dt = 1$
Solving $dx/dt = 1$ gives $x=t +s$
Solving $du/dt = 1$ gives $u=t+ s/2$
Solving $dy/dt = u$ gives $y = (1/2)t^2 + st/2 + s$
This is where I get stuck,
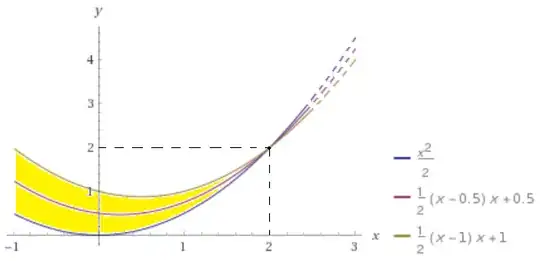
$t=x-s$ so $y = (1/2)(x-s)^2 + (1/2)s(x-s) + s$
and $0 \leq s \leq 1$ so am i correct in saying that the domain of definition is the region between $y = (1/2)x^2 $ and $y = (1/2)(x-1)^2 + (1/2)(x-1) + 1$