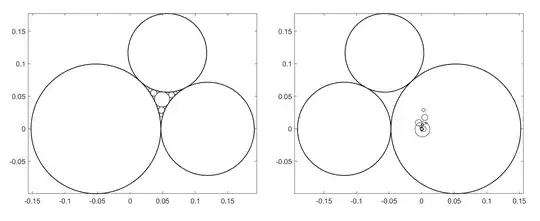
I'm working on a general Apollonian gasket (i.e., with no particular symmetry). One example might be to populate a Steiner chain with Apollonian circles. I programmed a recursive Descartes' theorem using the equations given in Wikipedia (Descartes' Theorem). I get a nice result for a sample case I set up; it's shown on the left of the figure below.
However, when I tried a test case from another part of the plane a got cockamamie results. To demonstrate this I took the original example, call it $Z$, and applied the same algorithm to $-Z^*$, i.e., the negative conjugate. The results are seen on the right of the figure below.
I'm trying to determine what's wrong here. Am I making an error? Is the complex Descartes' theorem of limited applicability? I can create a workaround by rotating the working area to the vicinity of the positive $x$-axis, but I'm really seeking to develop a robust algorithm.
Any insights or suggestions would be appreciated.