-1

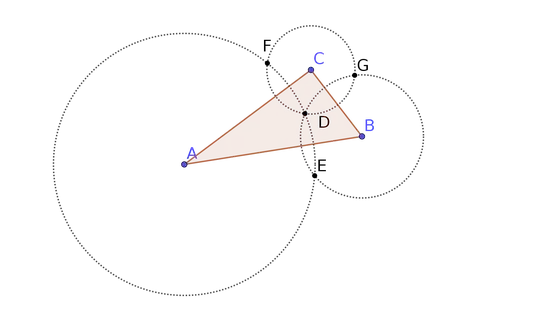
Given any triangle $\triangle ABC$, let us draw its orthocenter $D$. By means of this point, we can draw three circles with centers in $A,B,C$ and passing through $D$.

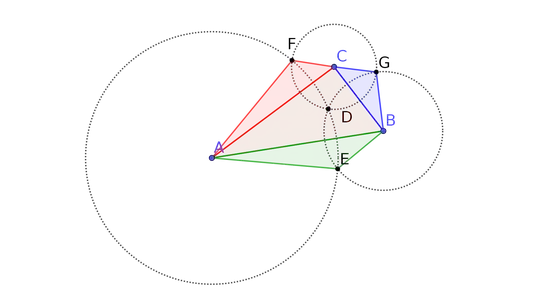
enter image description here

These circles intersect in the points $E,F,G$, which can be seen as the vertices of three triangles $\triangle AFC, \triangle CGB$ and $\triangle BEA$.

enter image description here

My conjecture is that

The sum of the areas of the triangles $\triangle AFC, \triangle CGB, \triangle BEA$ is equal to the area of the triangle $\triangle ABC$.

Furthermore,

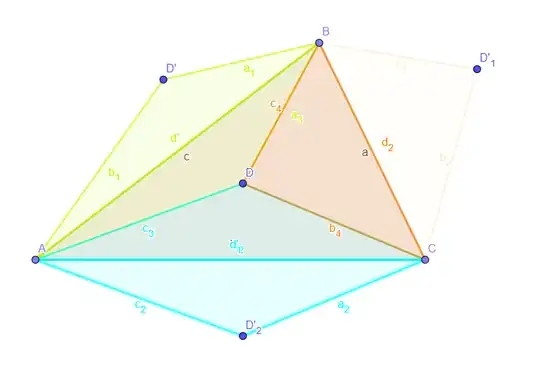
If we substitute the orthocenter $D$ with the centroid of $\triangle ABC$, then the areas of $\triangle AFC, \triangle CGB$ and $\triangle BEA$ are all equal, and their sum is equal to the area of the triangle $\triangle ABC$.

Maybe these are very well known theorems. However, is there a compact proof for such conjectures?

NOTE: These conjectures are very similar to the one exposed in this post.

Thanks for your help, and sorry for imprecision or triviality.

  • "If we substitute the centroid $D$ with the orthocenter [...], then the areas [...] area all equal ..." Not so! Consider a right triangle (or a very-nearly-right triangle, if you want to restrict yourself to acute figures). Two of the constructed triangles vanish (or are very small); the areas cannot all be equal, nor equal to the area of the original triangle. As greedoid has shown, the sum-of-areas gives the original area regardless of $D$'s location, so each area being equal to original triangle simply never holds. – Blue Nov 16 '18 at 10:58
  • @Blue Sure, sorry, I edit. I meant that the areas are all equal and their sum is equal to the area of the original triangle! –  Nov 16 '18 at 11:00
  • @Blue Thanks to point it out. –  Nov 16 '18 at 11:02
  • Open problem, the case of the othocenter yields to three equal areas. Why? Is this the only solution? –  Nov 16 '18 at 11:02
  • Orthocenter does not yield three equal areas. (Again, two areas are zero in the right-triangle case.) I think you're confusing orthocenter and centroid. The areas are definitely equal for the centroid. Keep in mind that, as greedoid's answer demonstrates, there's nothing super-special about these triangles. They're merely reflections of the sub-triangles determined by $D$ in the interior of $\triangle ABC$; so, any area properties can be discussed in terms of those interior triangles. The exterior ones are a distraction. – Blue Nov 16 '18 at 11:07
  • 1
    That the centroid is the only point making three equal areas is well-known. To see why it must be so, consider: If $\triangle ABD$ has one-third the area of $\triangle ABC$, then its height relative to base $\overline{AB}$ must be one-third that of $\triangle ABC$; thus, $D$ is on a line parallel to that base, one-third of the way "up". Likewise, $D$ is on other lines parallel to the other sides. These three (distinct) lines can have at most one point in common; the centroid is that point. – Blue Nov 16 '18 at 11:14
  • @Blue Yes, I am definitely confusing the terms. Hope I corrected now. Then the question is if the three triangles dissecting the original one, obtained starting from the centroids have the same area. Right? –  Nov 16 '18 at 11:15
  • Ok I see. Thanks, I didn't know this result. –  Nov 16 '18 at 11:16
  • 1
    You now have the correct question. But it's definitely a trivial one. :) – Blue Nov 16 '18 at 11:18
  • I see. Thanks anyway for the patience of correcting and explaining! –  Nov 16 '18 at 11:19

2 Answers2

1

This is true since for any point in triangle (not just centroid or orthocenter):

$ACF$ is congruent to $ACD$ (sss), ($AD = AF$, $CD=CF$, and common $AC$)

$ABE$ is congruent to $ABD$ (sss) and

$BCG$ is congruent to $BCD$ (sss).

nonuser
  • 91,557
  • Right! Thanks! Very neat. And what about the fact that the areas of the three external triangles are the same in case of the orthocenter? Is this the only case? –  Nov 16 '18 at 10:28
0

Given the arbitrary point D inside the triangle, if you get the symmetrical points with respect to all of the sides, the triangles built outside are congruent to those built inside. And the three of them divide perfeclty the area of the triangle. So the conjecture is correct.

enter image description here

Francesco Iovine
  • 301