Is the alternating sum of exp(-exp(n z)) analytic?

Question

Define $f(z) = \frac{1}{\exp(\exp(z))} - \frac{1}{\exp(\exp(2z))} + \frac{1}{\exp(\exp(3z))} - \frac{1}{\exp(\exp(4z))} + ...$

$$f(z) = \sum_{n = 1}^{\infty} (-1)^{n-1} \exp(-\exp(n z))$$.

Is $f(z)$ analytic anywhere in the complex plane, such that $f(z)$ converges to its Taylor series? Are there values of $z$ where $f(z)$ doesn't converge? For real$(z)>0$, is the function real analytic, infinitely differentiable?

This question is inspired by the stack exchange post: Is $\frac{1}{\exp(z)} - \frac{1}{\exp(\exp(z))} + \frac{1}{\exp(\exp(\exp(z)))} -\ldots$ entire?, where I tried to modify the function so as to emphasize the behavior of exp(-exp(z)).

Answer 1

Clearly the function $f(z)$ does not converge for $\operatorname{Re}(z)=0$. Hence the function is not entire and has no non-zero radius Taylor series when expanded at $\operatorname{Re}(z)=0$.

This is because $\exp(-\exp(nxi))$ for real $x$ and integer $n$ is just $\exp((-1)^{nx})$ and hence the terms of the series do not converge. And taking terms together does not help.

Thus the sum of those terms does not converge. The average of terms converges only weakly but that is a completely different function.

Notice that $\exp(nz)$ has a very simple limit for $n$ very large and $\operatorname{Re}(z)$ not equal to $0$.

If $\operatorname{Re}(z)>0$ and $f(z)$ is differentiable then it is termwise differentiable. This is consistent with the fact that the termwise differentiated $f(z)$ also converges for $\operatorname{Re}(z) > 0$, suggesting that it might be true that $f(z)$ is analytic for $\operatorname{Re}(z)>0$.

The terms decline exponentially for $\operatorname{Re}(z) > 0$ which also suggest it might be true that $f(z)$ is analytic for $\operatorname{Re}(z)>0$. (similar to fast declining real Fourier series within its period always being $C^\infty$ (=theorem !) ).

( @Sheldon : Btw this is partially similar logic as used by tommy1729's sinh method for tetration, however here we have no need for analytic continuation since we have convergeance already .. which is also another pro analytic argument. Imho tommy1729' sinh method is more complicated yet at the same time intuitive )

Answer 2

For $Re(z) \neq 0$ , substitute $t = \exp(z)$. (the case $Re(z) = 0$ does not converge without a summability method as already explained in my other answer)

Then we consider :

$$f(t) = \sum_{n = 1}^{\infty} (-1)^{n-1} \exp(-t^n)$$.

We rewrite that as :

$$f(t) = \sum_{j>-1} \sum_{n = 1}^{\infty} (-1)^{n-1} \frac{(-t^n)^j}{j!}$$.

and change the order of summation

$$f(t) = \sum_{n = 1}^{\infty} \sum_{j>-1}(-1)^{n-1} \frac{(-t^n)^j}{j!}$$

Now we see the problem is the case $j=0$ aka the constant $1$ terms of the exponentials.

Otherwise we could have made it analytic.

However by splitting $j$ in odd and even terms,

$$f(t) = \sum_{n = 1}^{\infty} \sum_{j>-1}(-1)^{n-1} \frac{(-t^n)^j}{j!}$$

becomes

$$f(t) = \sum_{n = 1}^{\infty} \sum_{j>-1}(-1)^{n-1} \frac{(t^n)^{2j}}{(2j)!} + \sum_{n = 1}^{\infty} \sum_{j>-1}(-1)^{n-1} \frac{-(t^n)^{2j+1}}{(2j+1)!}$$

and by doing the same with $n$ we get a well defined analytic Cesàro sum for all $z$.

More precisely, after splitting the $n$ in odd and even we simply apply the taylor formula

$$\frac{1}{1-t^v} = 1 + t^v + t^{2v} + t^{3v} + t^{4v} + t^{5v} + ...$$

which is valid for all $t$ not on the unit circle.

Answer 3

This is an answer to half the question, which is the case for real<0. For all real(z)<0, f(z) alternates between two different values, both of which are analytic. This is because $\exp(nz)=\exp(\Re(nz))\times\exp(\Im(nz))$, and $\Re(nz)$ gets exponentially close to zero as nz gets arbitrarily large negative. It doesn't matter what $\Im(z)$ is, because zero times anything is still zero. As $\exp(nz)$ approaches arbitrarily close to zero, $(-1)^n\exp(-\exp(nz))$ approaches arbitrarily close to one for n large and even, and it approaches arbitrarily close to negative one for n large and odd. One substitution one can make is $y=\exp(z)$

$f(y)=\sum_{n=1}^{\infty}(-1)^n\exp(-y^n)$

This can be expanded as a taylor series, for which the first few 20 terms are listed below. notice that here, f(y=0) alternates between 1 and 0 as n goes to even infinity and 0 as n goes to odd infinity. Alternatively, the terms $a_n$ terms for the taylor series of f(y) can be used as the coefficients for a $2\pi i$ periodic complex function $f(z)=\sum_{n=1}^{\infty}a_n\exp(nz)$. In "y", this function has a natural boundary of the unit circle. if |y|=1, and y^n doesn't repeat in an odd cycle, and does repeat in an even cycle. This condition is met if $\Re(z)=0$ and $\frac{\Im(z)}{2\pi}$ can be expressed as a rational number in simplest form, then if the denominator is even, there ia a singularity at z. Then f(y)=f(exp(z)) gets arbitrarily large since the (-1)^n terms are cyclic instead of cancelling. So singularities are dense on the boundary of the unit circle for $f(y)$, which corresponds to singularities being dense on the imaginary axis for the $2\pi i$ periodic version of f(z). These singularities are large for $\pi i$ and $\pi i/2$ but they get fairly tame quickly. Here are the first 20 terms of the Taylor series for f(y).

f(y)= 1/2 - (1/2)*(-1)^n
+y^ 1* -1
+y^ 2*  3/2
+y^ 3* -7/6
+y^ 4*  13/24
+y^ 5* -121/120
+y^ 6*  1201/720
+y^ 7* -5041/5040
+y^ 8*  18481/40320
+y^ 9* -423361/362880
+y^10*  5473441/3628800
+y^11* -39916801/39916800
+y^12*  338627521/479001600
+y^13* -6227020801/6227020800
+y^14*  130784734081/87178291200
+y^15* -1536517382401/1307674368000
+y^16*  9589093113601/20922789888000
+y^17* -355687428096001/355687428096000
+y^18*  10679532671808001/6402373705728000
+y^19* -121645100408832001/121645100408832000
+y^20*  1338095434054579201/2432902008176640000+...

One could arbitrarily define f(z) as the average of the even and odd cases, which would make $f(z=-\infty)=1/2$. In that case, $f(0)=\frac{1}{2e}$. Here are my conjectures about the function for real(z)>0, some of which I will attempt to prove in a later post.

• for $\Re(z)>0$ the limiting value for f(z) is only defined iff $\Im(z)=2n\pi i$
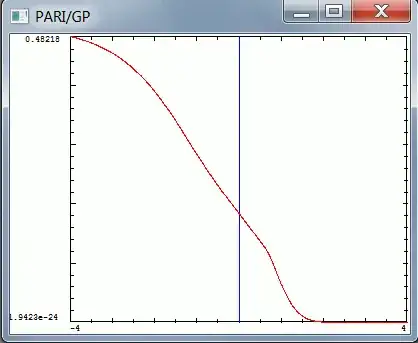
• for $\Im(z)=0$ and $\Re(z)>0$, f(z) is infinitely differentiable. But f(z) does not converge to its Taylor series. At the real axis for real(z)>0, it has a radius of convergence of zero, and is nowhere analytic.
• for z=0, f(z) converges to $\frac{1}{2e}$, and has the same taylor series for both the nowhere analytic function, and the boundary of the analytic function, provided one defines the function as the average of the two analytic functions.

Plot of f(z) at the real axis:

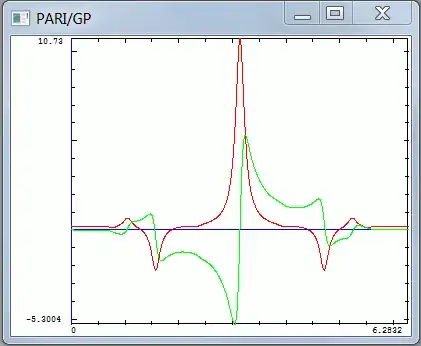
Plot of f(z) at real(z)=-0.1, from imag(z)=0 to imag(z)=2Pi, showing the influence of nearby singularities, at $\pi i$, $\frac{\pi i}{2}$, $\frac{3\pi i}{2}$. Red is real and green is imaginary.