I want to prove that a solution $y(x)$ of the IVP: $$y'=y^2+\cos x^2, \quad y(0)=0 $$ exists, with $0\leq x \leq \frac12$.
Picard says that there exists a solution for $x \in (-\delta,\delta)$, for some $\delta>0$ , but $[0,\frac12]$ is closed and not symmetric around zero. How can I restrict $(-\delta,\delta)$ to show this?
You can only have a finite end point in the domain $(a,b)$ of the maximal solution if the solution con/diverges towards the boundary of the domain of the differential equation for $x\to b$. As that domain is the full $\Bbb R^2$ this can only happen if the solution has a pole at $x=b$ where it diverges towards infinity.
Over this maximal domain the solution satisfies the differential inequality as long as the bounding functions are defined, $$ y^2\le y'\le y^2+1\implies \frac{y_c}{1-y_c(x-c)}\le y(x)\le \tan(x+\arctan(y_0)). $$ The second relation tells us that the solution is finite for $x<\frac{\pi}2-\arctan(y_0)$. With the given initial conditions this includes the interval $[0, \frac32]$.
As Riccati equation the solutions can be represented as $y=-\frac{u'}u$ with $u''+\cos(x^2)u=0$, $u(0)=1$, $u'(0)=0$. Then the pole is at the first posiitive root of $u$. The numerical solution is
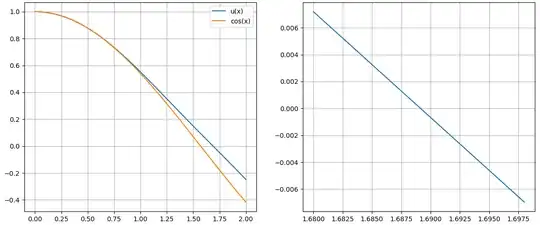
where the right is a zoom into the left plot. This shows the root of $u$ and thus the pole of $y$ in the interval $[1.6875, 1.69]$.
On the theoretical side, the Sturm-Picone comparison theorem tells us that between the roots $-b,b$ of the even function $u$ there must be at least a half-period of the solution $v(x)=\cos(x)$ of $v''+v=0$, as $\cos(x^2)<1$. This again confirms $b>\frac\pi2$.
