Exercise 1:
a) Determine all of the units in $\Bbb Z\Big[\frac{1+\sqrt{-3}}{2}\Big]$.
b) Determine all of the units in $\Bbb Z[\sqrt{-6}]$
I know that the units for a) are $\pm 1, (\pm 1 \pm \sqrt{–3})/2$, because their norms all equal $1$ or $-1$. But how do I prove that these are the only six solutions?
Thank you
Hint: The norm of $a+b\omega$ is $(a+b\omega)(a+b\bar\omega)=a^2+b^2+ab$.
Ok, I just covered norms, and I had similar questions, but I think I'm starting to figure this out.
I might suggest https://math.stackexchange.com/a/2968442/114910 and https://math.stackexchange.com/a/2553023/114910 and I'm sure there are others.
So Artin points out there are infinitely many solutions (to find units) in a real quadratic field:
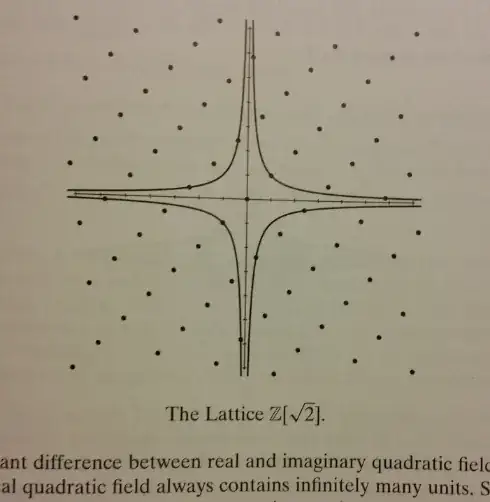
He's pointing out the solution (to find units) to a real quadratic field is a hyperbola $ax^2-by^2=c$ (actually, not quite so simple, but hold on a minute). When you have an imaginary quadratic field, the solution is going to be some kind of ellipse $ax^2+by^2=c$, so there can only be finitely many solutions (this isn't quite right, but hold on).
Of course, this solution you're figuring out comes from the norm.
$$N(\alpha)=\alpha\overline{\alpha}$$
and for a unit, $N(\alpha)$ always equals $\pm 1$.
For the problem at hand, $\mathbb{Z}[\sqrt{-6}]$, then $N(\alpha) =\alpha\overline{\alpha} = a^2 + 6b^2$. Part of my confusion was forgetting that $a,b \in \mathbb{Z}$, this is probably stated at the beginning somewhere and then just never mentioned again. What that means is you're looking at an ellipse $a^2 + 6b^2 = 1$ and the solutions will be your units.
When I was talking about the hyperbola I said my explanation wasn't quite right. That hyperbola is actually a mapping from the field you're looking at to the reals, but I think it gave me a better understanding of where these unit solutions come from. But what that means is you're actually looking for solutions to an equation that equals $\pm 1$. So to correct the above, you're looking for solutions of a,b where
$$ a^2 + 6b^2 = \pm 1, a,b \in \mathbb{Z} $$
The restriction to the (real) integers makes things easy though, you can see if b is any integer then there is no solution for a. So the only solutions are $\pm 1 \in \mathbb{Z}[\sqrt{-6}]$.
That was the easier one, the other example you asked about is simply a bit more algebra. Start with
$$ \mathbb{Z}[\frac{a}{2}+\frac{b\sqrt{-3}}{2}, a,b \in \mathbb{Z}] $$
And go through the same steps. You'll see that $N(\alpha) = \frac{a^2}{4}+\frac{3b^2}{4}$, and since you're looking for units you know $N(\alpha) = \pm 1$, or rearranged a bit
$$ a^2 + 3b^2 = \pm 4, a,b \in \mathbb{Z} $$
This is once again an ellipse, so there are only finitely many solutions. Hopefully it's obvious if $a>2$ there are no solutions for $b$, and likewise, if $b > \sqrt{\frac{4}{3}}, b \in \mathbb{Z}$ there aren't solutions for $a$. This should get you the required solutions, but remember to apply them back into your definition correctly, for example, one solution to the ellipse is $a=2,b=0$ which gives $1 \in \mathbb{Z}[\frac{a}{2}+\frac{b\sqrt{-3}}{2}, a,b \in \mathbb{Z}]$, I think you should be able to get the rest from here.
