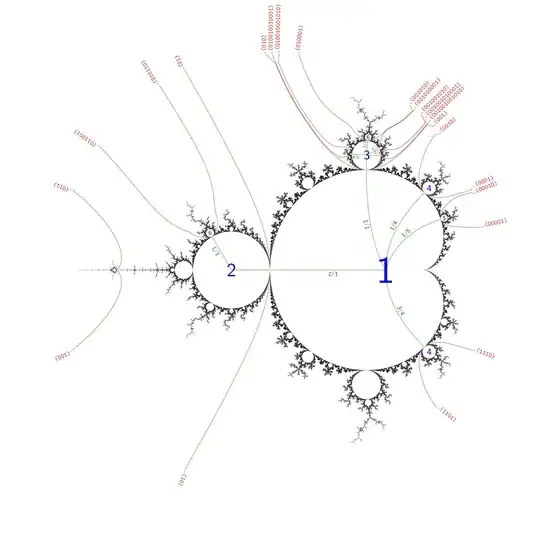
Taking a look to the picture of the Mandelbrot set, one immediately notice its biggest component which we call the main cardioid. This region is composed by the parameters $c$ for which $p_c$ is hyperbolic when its periodic point is a fixed point (that is whose period is $n=1$). It turns out that these parameters are all of the form $$ c_{\mu}:=\frac {\mu}2\left(1-\frac {\mu}2\right) $$ when $\mu$ runs in the open unitary disk $\Delta_1$.
For every rational number $\frac pq$ ($p,q$ coprime), there is a circular shaped "bulb" tangent to the main cardioid at the point $c_{\mu}$ for $\mu=e^{2\pi i\frac pq}$, called the $\frac pq$-bulb (clearly $0\le\frac pq\le1$), consisting of all parameters $c$ whose polynomial $p_c$ admits $q$-periodic points.
The best current estimate known was proved by Yoccoz in the Hubbard paper Local connectivity of Julia sets and bifurcation loci: three theorems of J.C.Yoccoz, which states that the diameters of the $\frac pq$-limbs tends to zero like $1/q$. Nonetheless numerical experiments suggest the following conjeture:
The diameter of the limbs tends to zero like $1/{q^2}$.
Or maybe one can consider a broader problem:
Is the Yoccoz asymptotics $1/q$ sharp, or can it be improved?
Some questions for you:
-It is clear that we have different bulbs with the same denominator $q$; are they all the different circles tangents to the main cardioid, which have the same radius depending on $q$?
-In Wikipedia it seems that the same object is first called bulb, then called limb: are these only different names for the same object?
-it seems that these bulbs are exact circles; is this true for all of them?
I ask this because studying the decay rate of the diameter of the $\frac pq$-limbs, if we fix $q$ and we call $p_1,\dots,p_n$ all the integers coprime with $q$ (and $\le q$), it would be nice if all the $\frac{p_1}q,\dots,\frac{p_n}q$-limbs have exactly the same diameter. Then the question of ratio decay would be sharper defined (and I'm not sure if it is actually necessarily for the question to be well defined).
EDIT We can put concepts in order as follows:
There is a unique region $\Omega_0$ composed by the parameters $c$ for which $p_c$ is hyperbolic when its periodic point is a fixed point (that is whose period is $n=1$). It turns out that $\Omega_0$ is bounded by the main cardioid and the parameters composing $\Omega_0$ are all of the form $$ c_{\mu}:=\frac {\mu}2\left(1-\frac {\mu}2\right) $$ when $\mu$ runs in the open unitary disk $\Delta_1$. For every rational number $\frac pq$ (such that $0<\frac pq<1$ and $p,q$ coprime), we define the $\frac pq$-limb $M_{\frac pq}$ as the connected component of $M\setminus\overline{\Omega_0}$ tangent to the main cardioid at the point $c_{\mu}$ for $\mu=e^{2\pi i\frac pq}$; the biggest circular shaped "bulb" in $M_{\frac pq}$, called the $\frac pq$-bulb and denoted as $\Omega_{\frac pq}$, consists of all parameters $c$ whose polynomial $p_c$ admits $q$-periodic points.
We note that even though the boundary of the bulb $M_{\frac12}$ %period $2$ hyperbolic component of the Mandelbrot set is a perfect circle of radius $\frac14$ centered at $-1$, not all the bulbs are circles; see the case of the bulbs of period $3$.
Do you see contradiction/errors/wrong definitions?