If I have a regular dodecahedron and construct lines between the center of the dodecahedron and its vertices. How do I calculate the angle between such lines, subtended by an edge? This picture can probably better explain what I meant
For now, I am thinking of calculating the radius of the circumscribed sphere and then using cosine law to find out the angle. Is there a more straightforward way?
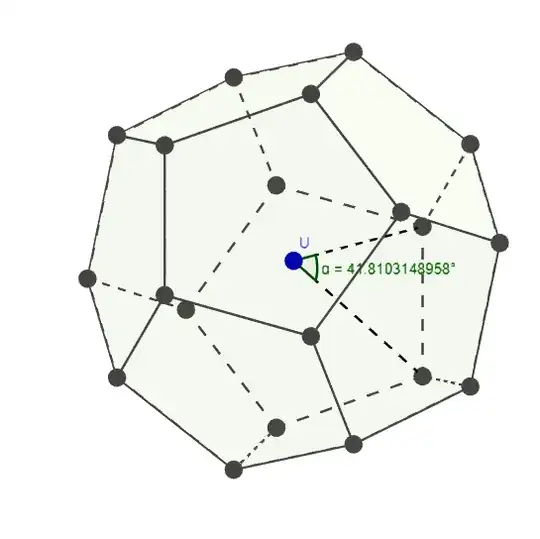
There is an inscribed cube in a regular dodecahedron, which will aid the calculation of the radius of the circumscribed sphere.
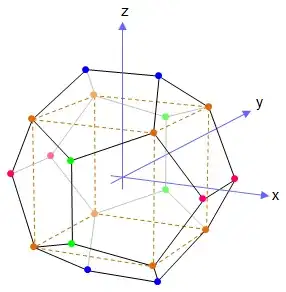
Assume the regular dodecahedron has edge length $1$. The edge of the cube is the diagonal of a unit regular pentagon:
$$\begin{align*} \text{Side of cube} &= \text{Diagonal of a pentagon face}\\ &= \frac{1+\sqrt 5}2\\ &= \varphi \end{align*}$$
The diameter of the circumscribed sphere is the space diagonal of that inscribed cube, which is just $\sqrt 3$ times the side length of the cube:
$$\begin{align*} \text{Diameter of sphere} &= \sqrt 3\cdot \text{Side of cube}\\ &= \sqrt 3\varphi\\ \text{Radius of sphere} &= \frac{\sqrt3}2\varphi \end{align*}$$
As in the diagram in the question, using cosine law with a triangle formed by the sphere centre and an edge of the dodecahedron:
$$\begin{align*} \cos\alpha &= \frac{r^2 + r^2 - 1^2}{2r^2}\\ &= \frac{2 - r^{-2}}{2}\\ &= \frac{2-\frac43\varphi^{-2}}{2}\\ &= \frac{2-\frac23(3-\sqrt5)}{2}\\ &= \frac{\sqrt5}3\\ \alpha &\approx 41.81^\circ \end{align*}$$
The plane passing through two opposite edges of the dodecahedron is a bisector of the angle between two adjacent faces. From here you can begin to work with regular pentagonal pyramid.
If you are willing to believe Wolfram Cloud Sandbox the following code
With[{vc = PolyhedronData["Dodecahedron", "VertexCoordinates"]},
ArcCos[Dot[vc[[1]], vc[[14]]]/Norm[vc[[1]]]^2] // FullSimplify]
returns the result $\, \textrm{arcsec}(3/\sqrt{5}) = \textrm{arcsin}(2/3)\,$ which translates to $\,\approx 0.729727 \approx 41.8103^\circ.$
First off, you drew a dodecahedron. "Hedron" means "face" and the thing with the pentagonal faces has 12 faces and 20 vertices, not the other way around.
Think of the dodecahedron as projected radially onto the sphere in which it is inscribed. Let $A$ and $B$ be any two adjacent vertices and draw a spherical triangle whose vertex $C$ is the center of a pentagon's face having $AB$ as one of itscedges.
Angle $A$ measures half the angle at the vertex, which in the spherical projection means it measures $60°$. Ditto for angle $B$. Angle $C$ measures one fifth of a revolution $=72°$. From the angles of the triangle you can get the arcs using the spherical Laws of Cosines [sic; there are two to choose from] and then arc $AB$ measures the central angle you want.
You may also want to repeat this with $AB$ as a face diagonal instead of an edge, and compare your result with the edge of a cube.
I take reference to the pic provided in the answer of peterwhy, esp. its colorcoding.
The edge length is provided by the vertical distance of the 2 neighbouring green vertices. The height of the incribed cube, i.e. the distance of the orange vertices, is $\varphi$ times as large (the golden ratio, $\varphi=\frac{1+\sqrt{5}}{2}$). The vertical distance between the 2 blue vertices then will be $\varphi^2$.
The angle $\alpha$ then is just the center angle of that rectanle with all 4 blue vertices. Alternatively you will have $1:\varphi^2=\tan(\frac{\alpha}{2})$ or, solving on the searched for quantity, $\alpha=2\arctan(\varphi^{-2})=41.81...°$.
--- rk
