7

I need to demonstrate that there is a finite set of planar graphs with the property that the graph G is isomorphic with its complement graph.Can you give me some suggestions or hints ?Thank you

Andrew Uzzell
  • 1,711
user910
  • 383
  • 4
  • 8

1 Answers1

7

I apologize for posting the full answer. Somehow I missed that you only need hints. I'll leave the full answer below and give few hints here.

  • Hint 1 How many edges does a self-complementary graph have?
  • Hint 2 What are the implications of Euler formula for planar graphs?

Full Solution follows.

Let $G$ be a self-complementary graph of order $n.$ Then $G$ has $\frac{n(n+1)}{4} = \mathcal{O}(n^2)$ edges. But from Euler's formula, every planar graphs has $\mathcal{O}(n)$ edges. Hence there are only finitely many self-complementary planar graphs.

To be more precise, Euler's formula implies that for a planar graph $G$ of order $n \geq 3$ we have $$|E(G)| \leq 3n-6$$ hence if $G$ is self complementary we have $$ \frac{n(n+1)}{4} \leq 3n-6$$ which implies $3 \leq n \leq 8.$ Hence a self-complementary planar graph may have at most 8 vertices.

As it appears there are only 14 such graphs and they can be seen in the attached figure!

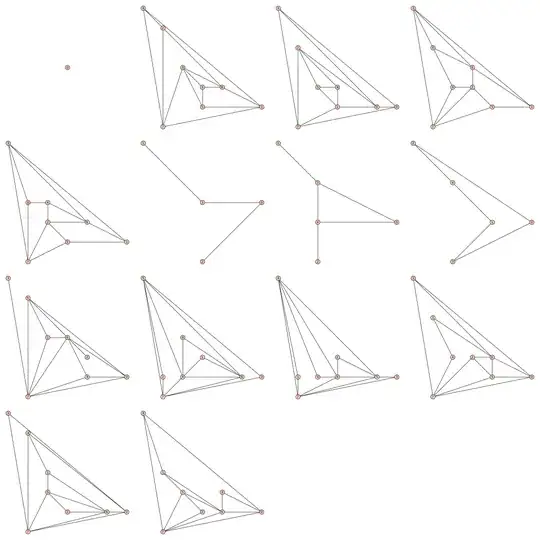
enter image description here

Jernej
  • 5,170
  • 2
    Nice enumeration. Still three remarks: 1. A selfcomplementary graph has $n(n-1)/4$ edges and not $n(n+1)/4$. You then derive $3\leq n\leq 10$ from this. 2. Every sequence in $\mathcal O(n)$ is also in $\mathcal O(n^2)$. What you actually want to say is that the edge count of self-complementary graphs is in $\Omega(n^2)$, but the edge count of planar graphs is in $o(n^2)$, which are disjoint. 3. It can be argued to include the empty graph in the list. – M. Winter Aug 11 '17 at 15:47
  • The correct case analysis (see above Comment by @M.Winter) requires us to consider $n=9$ (since $n(n-1)/4$ is an integer when $n\equiv 0,1 \bmod 4$). There are no such solutions, but it is not an obvious conclusion. Fortunately pertinent references are given in Answer to this previous Question. – hardmath Aug 12 '17 at 00:08