Finding all possible paths in graph with matrix

Question

Let's assume we have a one-direction graph and we want to produce a matrix that represents relations:

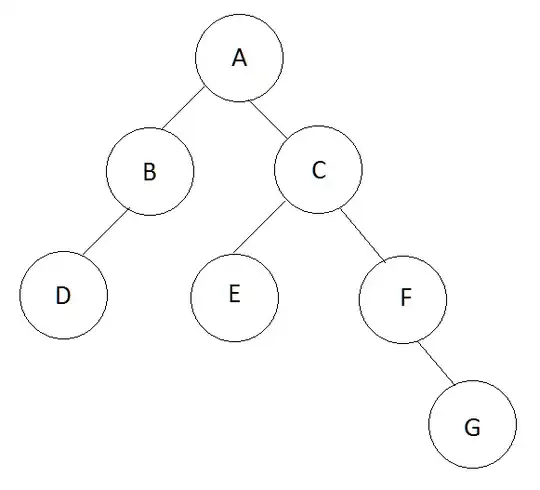
the structure of graph image

At first step we have only a matrix that contains straight relations, so for given image we have this matrix:

    A    B    C    D    E    F    G
A   1    1    1    0    0    0    0
B   0    1    0    1    0    0    0
C   0    0    1    0    1    1    0
D   0    0    0    1    0    0    0
E   0    0    0    0    1    0    0
F   0    0    0    0    0    1    1
G   0    0    0    0    0    0    1

Now I want a way to calculate final matrix in a way that for each node, if there is any path to destination node, it has 1 else 0 in the matrix:

    A    B    C    D    E    F    G
A   1    1    1    1    1    1    1
B   0    1    0    1    0    0    0
C   0    0    1    0    1    1    1
D   0    0    0    1    0    0    0
E   0    0    0    0    1    0    0
F   0    0    0    0    0    1    1
G   0    0    0    0    0    0    1

If we call the first matrix A, what should I do to achieve the second matrix?

score 2 · Accepted Answer · edited May 27 '22 at 04:23

2

I found that if we calculate A^n (where n is the number of nodes), we find a new matrix that has some 0 values and some positive ones. If we replace each positive number with 1, the final matrix will be produced.

edited May 27 '22 at 04:23

AtomicSource

3

answered Sep 16 '18 at 05:37

Amin Mozhgani

131

This proves your claim: https://math.stackexchange.com/questions/2434064/proof-raising-adjacency-matrix-to-n-th-power-gives-n-length-walks-between – algebroo May 27 '22 at 05:06

Finding all possible paths in graph with matrix

1 Answers1