1

I have an 8 dimensional dataset (as an Nx8 matrix), and I am hypothesising that much of the dataset can be described simply by linear addition of two known non-orthogonal vectors (i.e. two 1x8 vectors).

As a result I want to project the data onto a skew coordinate system which lies on a 2D plane embedded within the larger 8-D space.

If the two vectors are orthogonal I am aware that it is a simple matrix multiplication of the Nx8 matrix by the 2x8 matrix (the two vectors together). For example consider the 3D simplification shown below. My data is analagously described by a Nx3 matrix along the x,y & z axes. However I want to project into onto the 3D skew coordinate system in red, described by the known vectors a and b. 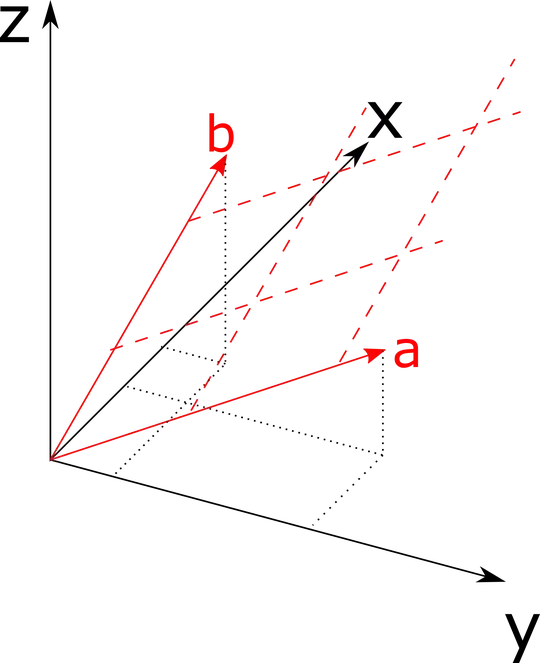a 3D simplification of the 8D problem in the question My two questions are:

1) What is the analogous operation to project the 8D data onto a skewed 2D coordinate system?

2) If I perform the matrix multiplication described above with the non-orthogonal vectors what is the geometrical interpretation of the resultingNx2 matrix?

AlexLipp
  • 165
  • 1
  • 6
  • You may calculate the SVD of your matrix and then check, wether two of the singular values are dominant. – denklo Sep 05 '18 at 14:42
  • @denklo I have performed PCA (via SVD) and the first two principle components do account for a dominant proportion of the variation. However the actual vector loadings of the principal components are required to be orthogonal, and the two externally derived vectors I want to project the dataset onto are not (but are subparallel to the PCs). Thus, whilst simply extracting the first two principal components would approximate what I wish to do, I would like to exactly describe the dataset in terms of the two vectors. – AlexLipp Sep 05 '18 at 14:48

1 Answers1

2

1)

(I'm using geometric algebra.)

You can take the wedge product $I = a\wedge b$ to represent the plane. Then any vector $v$ can be decomposed into components parallel and perpendicular to the plane:

$$v = v_\parallel + v_\perp$$

$$v_\parallel = I^{-1}(I\cdot v)$$

$$v_\perp = I^{-1}(I\wedge v)$$

You can get the coefficients of $v_\parallel$ with respect to the basis $\{a,b\}$ by taking dot products with the dual basis $\{a^*,b^*\}$ :

$$a^* = bI^{-1},\quad b^* = -aI^{-1}$$

$$v_\parallel = v_a a + v_b b$$

$$v_\parallel\cdot a^* = v_a(a\cdot a^*) + v_b(b\cdot a^*) = v_a(1) + v_b(0) = v_a$$

$$v_\parallel\cdot b^* = v_a(a\cdot b^*) + v_b(b\cdot b^*) = v_a(0) + v_b(1) = v_b$$

Alternatively, using matrix algebra:

Take $M$ to be the $8\times2$ matrix with columns $a$ and $b$. If I remember correctly, the projection is

$$v_\parallel = M(M^TM)^{-1}M^Tv$$

and the coordinates are

$$\begin{bmatrix} v_a \\ v_b \end{bmatrix} = (M^TM)^{-1}M^Tv$$

2)

The $N\times2$ matrix product is composed of dot products $v\cdot a,\;v\cdot b$ ; these are the coordinates with respect to the dual basis. If $a$ and $b$ are orthonormal, then $a^* = a$ and $b^* = b$, so this also gives the coordinates $v_a,\;v_b$.

mr_e_man
  • 5,986
  • Thank you! I'm sorry I'm not particularly familiar with formal geometric algebra, would you be able to elaborate on the difference between a and a* (and equally b and b*). – AlexLipp Sep 05 '18 at 15:28
  • The dual basis is defined such that $a\cdot a^* = b\cdot b^* = 1,;a\cdot b^* = b\cdot a^* = 0$. This makes computations almost as easy as with an orthonormal system. – mr_e_man Sep 05 '18 at 15:31
  • I guess the matrix for the dual basis would be $(M^TM)^{-1}M^T$, or the transpose of that. – mr_e_man Sep 05 '18 at 15:38