5

Let $p_1$ and $p_2$ be twin primes, and let $p_1-1=a_1\times b_1$ and $p_2+1=a_2\times b_2$ be such that $|b_1-a_1|$ and $|b_2-a_2|$ are minimised. Similarly, let $p_1+1=p_2-1=a\times b$ be such that $|b-a|$ is minimised.

Now assume the twin prime conjecture, and let $$\mathcal P_n=\frac{\#\text{twin primes} \le n:\min\{|b_1-a_1|,|b-a|,|b_2-a_2|\}\neq|b-a|}{\#\text{twin primes} \le n}$$ What is the value of $\mathcal P_\infty$?

Note that by convention the pair $(2,3)$ are not twin primes.

For twin primes less than $100$, we have that $p_1=5,17$. Hence I think that if there are infinitely many such primes then they will be exceedingly sparse.

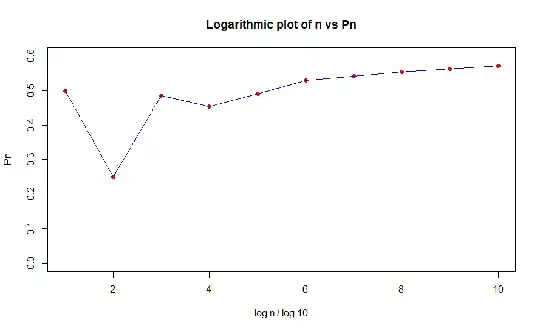
Here is a table showing $\mathcal P_n$ for increasing values of $n$. Credits to Enzo Creti for running the program. $$\small\begin{array}{c|c}\log_{10}n&1&2&3&4&5&6&7&8&9&10&11\\\hline \mathcal P_n&\frac12&\frac14&\frac{17}{35}&\frac{93}{205}&\frac{600}{1224}&\frac{4326}{8169}&\frac{31939}{58980}&\frac{243876}{440312}&\frac{1928700}{3424506}&\frac{15661079}{27412679}&\frac{129632703}{224376048}\\\hline\text{decimal}&\small 0.5&\small0.25&\small0.4857&\small0.4537&\small0.4902&\small0.5296&\small0.5415&\small0.5539&\small0.5632&\small0.5713&\small0.5777\end{array}$$

This can be seen more clearly in the following plot; more interesting is the behaviour after $n=10^4$.

enter image description here

There is a slight dip at $n=10^2,10^4$ but otherwise it looks like there is a converging increase in $\mathcal P_n$. It is unlikely, but if there reaches a point where $\mathcal P_k=\mathcal P_{k+1}$ then the twin prime conjecture will be disproved.

Community
  • 1
TheSimpliFire
  • 28,020
  • Hmm, happens more often after $100$. $p_1 \in {101, 107, 137}$ for example. – Daniel Fischer Sep 02 '18 at 19:12
  • 1
    As long as you only want to go up to a moderate limit, modify a Sieve of Eratosthenes to record a prime factor of each number (the smallest or the largest would be natural choices). That way, you get the factorisation of every number very cheaply, and with the prime factorisation it's easy to find the factors closest to the square root. If you want to look at large numbers, it won't be so easy. Factoring in general is hard. – Daniel Fischer Sep 02 '18 at 19:23
  • you can use this construct an artificial number system where this is true, then you will find even there it will not hold. try. – Nick Sep 02 '18 at 19:43
  • Hmmm, the sequence $5,17,101,107,137\ldots$ is not (yet) in the OEIS. – Barry Cipra Sep 03 '18 at 01:19
  • 1
    Made a very simple Sage program to find them. – Yong Hao Ng Sep 03 '18 at 05:01
  • 3
    Hopefully I didn't make any mistakes. It can handle up to $10^7$ easily, after which it's quite slow. At $10^7$ it fetches $31939$ passes out of $58980$ twin primes which is about 50%. It fetches a similar ratio for $10^3,10^4,\cdots,10^7$. – Yong Hao Ng Sep 03 '18 at 05:07
  • The numbers need more digits and more testing. Candidates are $\frac{1}{\sqrt3}$ , eulers gamma and even this number "T" divided by $3$.

    https://math.stackexchange.com/questions/4664497/simplifying-a-complicated-continued-fraction-expression?noredirect=1&lq=1

    And that is assuming it converges to a nonzero value.

     – mick Sep 03 '24 at 20:02
  • What happens if $p_1,p_2$ are just required to be $5 \mod 6,1 \mod 6$ rather than being prime ?? – mick Sep 03 '24 at 20:28
  • What is the expected MAX GAP between prime twins ? $\ln(x)^4$ ?? – mick Jun 04 '25 at 23:28

1 Answers1

0

Twin primes other than $3,5$ are of the form $6k\pm1$, which makes $p_1-1 = 6k-2$, $p_2 + 1 = 6k+2$, and $p_1+1 = p_2-1 = 6k$. Define $f(x) = \min\{|a-b|\}$ where $a b = x$, and you are asking are there infinitely many $k$ where $6k\pm1$ are both primes, and $f(6k-2) < f(6k)$ or $f(6k+2) < f(6k)$.

Experimentally, about $54\%$ of the twin primes are "close", not the $33\frac13\%$ that one would naively expect. Still, most likely infinitely many.

TheSimpliFire
  • 28,020
gnasher729
  • 10,611
  • 20
  • 38