I was searching for a solution to a very practical problem asked by a friend of mine. The problem was that he had to lay a dropped kerb to allow vehicular access to customer's property... except the kerb was on a road bend. Since I am the closest person that he knows to qualify as a civil engineer, so he asked me to find a formula that could be used for this purpose. In the image is a diagram with workings to create the final formula for the unknown radius. My question is this: Is the formula and derivation universally correct? 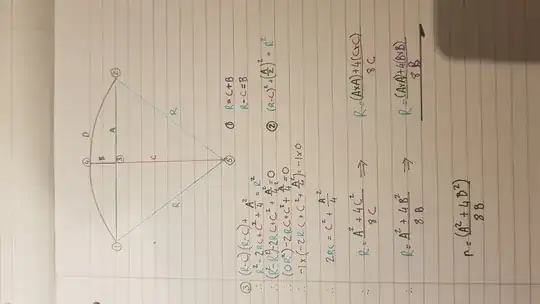
My result was $$r=\dfrac{4B^2+A^2}{8B}$$ Where B is the perpendicular height from midpoint of arc to midpoint of chord and A is the length of the chord itself.
I am concerned that I introduced an error in part 2 of the 3 steps of evaluation. Can anyone refute this?