2

Is it accurate to say that a Trapezoidal Riemann Sum includes one more term than the corresponding Left, Right, or Midpoint Riemann Sum? Using the following notation for the latter three:

Riemann Sums There are three types of Riemann Sums.

Right Riemann: $$ A = \frac{b-a}{n} [f(x_1) + f(x_2) + f(x_3) + \dotsb + f(x_n)] $$ Left Riemann: $$ A = \frac{b-a}{n} [f(x_0) + f(x_1) + f(x_2) + \dotsb + f(x_{n-1})] $$ Midpoint Riemann: $$ A = \frac{b-a}{n}[ f(x_{1/2}) + f(x_{3/2}) + f(x_{5/2}) + \dotsb + f(x_{n-1/2}) ] $$ (Original image here.)

My understanding is that the Trapezoidal Sum is given by $$ A = \frac{b\ -\ a}{n} \left[ \frac{1}{2}f(x_0) + f(x_1) + f(x_2) + f(x_3) + \dotsb + f(x_{n-1}) + \frac{1}{2}f(x_n) \right] $$

This might be seen, then, as a second compromise between the Left and Right Riemann Sum formulas (the Midpoint formula being the first), copying the terms they “agree upon,” and adding half of each of the two unique terms. Is this correct, and if so, why does this striking similarity to the Left and Right Riemann Sum formulas arise? I can follow the algebraic derivation from the trapezoid area formula, but I find it bizarre that the result would so closely mirror the Left and Right Riemann Sum formulas, despite its geometric picture being completely different.

user10478
  • 2,118
  • Also somewhat counterintuitive is the fact that the mid-point sum typically is more accurate than the trapezoidal approximation discussed here – RRL Aug 26 '18 at 00:21
  • Thanks for the link. Maybe someone can translate that into a less formal intuition. – user10478 Aug 26 '18 at 02:13

1 Answers1

2

The algebraic reason for the form of the sum in the trapezoid method is that a single trapezoid in that method has two base lengths: $f(x_i)$ on the left and $f(x_{i+1})$ on the right. Its height (measured horizontally, because in a trapezoid the "height" is always the distance between the parallel sides) is $h = \frac{b-a}n.$ Hence its area is $$ \frac12 h(f(x_i) + f(x_{i+1})) = \frac{b-a}n\left(\frac12 f(x_i) + \frac12 f(x_{i+1})\right). $$ When the areas of two adjacent trapezoids are added, the result is \begin{multline} \frac{b-a}n\left(\frac12 f(x_i) + \frac12 f(x_{i+1})\right) + \frac{b-a}n\left(\frac12 f(x_{i+1}) + \frac12 f(x_{i+2})\right) \\ = \frac{b-a}n\left(\frac12 f(x_i) + f(x_{i+1}) + \frac12 f(x_{i+2})\right). \end{multline} That is, the term $f(x_{i+1})$ comes from the sum of two copies of the term $\frac12 f(x_{i+1}).$ Add up the areas of all of the trapezoids, and all the terms will simplify in this way except for the first and last terms.

But we can also interpret this geometrically.

Consider a single trapezoid from the trapezoid method. We can dissect the trapezoid and rearrange the pieces into two half-width rectangles as shown in the figure below. On the left side of the figure, the shaded region is the original trapezoid. On the right side, the shaded region comprises the two half-width rectangles. To get from the left-hand shape to the right-hand shapes, we cut the triangle labeled $A$ out of the trapezoid and paste it into the region labeled $B.$

enter image description here

Now let's do that for each of the trapezoids in a trapezoid-method integral. On the left side of the figure below, the shaded region comprises all the trapezoids from the trapezoid method. We cut out the shaded triangles and use them to fill the unshaded regions. This produces many half-width rectangles, but most of the rectangles come in pairs of equal height. If we then erase the line separating each pair of equal-height rectangles, we get the arrangement of rectangles on the right side of the figure.

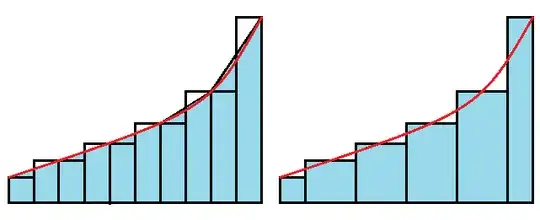
enter image description here

Now look at the rectangles on the right side of the figure. The leftmost rectangle is one half of the leftmost rectangle of the "left" Riemann sum and the rightmost rectangle is one half of the rightmost rectangle of the "right" Riemann sum. The other rectangles could be the last $n - 1$ rectangles of the "left" sum shifted half their width to the left, or they could be the first $n - 1$ rectangles of the "right" sum shifted half their width to the right. But the entire area of the rectangles on the right-hand side is exactly the area of the trapezoids on the left-hand side, merely with a finite number of pieces rearranged.

David K
  • 108,155
  • This is a wonderful answer! I just have one question; given the lower-right figure, it looks like the half-indexes from the Midpoint formula should be used for the middle (2nd, 3rd, 4th, and 5th) rectangles, since the curve ends up passing through their center. Why is this not reflected in the actual formula? – user10478 Aug 26 '18 at 18:21
  • 1
    The right-hand figure does have a lot in common with the midpoint method, except that once again all the rectangles are shifted half a place horizontally. Look at where the vertical edges of the rectangles cross the red curve in the lower-right figure; in the midpoint method, that is where the top of each rectangle would cross the curve horizontally, and the vertical edges of the rectangles from the midpoint method would cross vertically through the midpoints of the rectangles you see now. – David K Aug 27 '18 at 00:22
  • 1
    But you could look at the lower-right figure like this: we integrate the interval $[a,a+\frac h2]$ with a single rectangle under the "left sum" rule; we integrate $[b-\frac h2,b]$ wtih a single rectangle under the "right sum" rule; and we integrate $[a+\frac h2,b-\frac h2]$ with $n - 1$ rectangles of width $h$ using the midpoint rule. It's those $\frac h2$ terms in the bounds of the interval that put everything out of step with the regular midpoint rule, which goes in steps of width $h$ over the interval $[a,b].$ – David K Aug 27 '18 at 00:26