I have:
$$\bigwedge_{i=1}^{9} \bigwedge_{n=1}^{9} \bigvee_{j=1}^{9}~p(i,j,n)$$
I want to rewrite it so that to make the bottom part look like i=1 j=1 n=1 and also p(i,j,n) look as is now. I want to rewrite another part of this proposition so that it will be equal to the original proposition.
I mean this part that is visible below shold stay as is. All other part can be changed but the result should be equal to original (above proposition).
Additional info if needed (was asked in comments):
From the book: I am reading "Discrete Mathematics and Its Applications, 7th ed" p.33.
This is from Sudoku solving using SAT method.
From book:
To encode a Sudoku puzzle, let p(i, j, n) denote the proposition that is true when the number n is in the cell in the ith row and j th column. There are 9 × 9 × 9 = 729 such propositions, as i, j , and n all range from 1 to 9. For example, for the puzzle in Figure 1, the number 6 is given as the value in the fifth row and first column. Hence, we see that p(5, 1, 6) is true, but p(5, j, 6) is false for j = 2, 3, . . . , 9.
Given a particular Sudoku puzzle, we begin by encoding each of the given values. Then, we construct compound propositions that assert that every row contains every number, every column contains every number, every 3 × 3 block contains every number, and each cell contains no more than one number. It follows, as the reader should verify, that the Sudoku puzzle is solved by finding an assignment of truth values to the 729 propositions p(i, j, n) with i, j , and n each ranging from 1 to 9 that makes the conjunction of all these compound propositions true. After listing these assertions, we will explain how to construct the assertion that every row contains every integer from 1 to 9.We will leave the construction of the other assertions that every column contains every number and each of the nine 3 × 3 blocks contains every number to the exercises.
For each cell with a given value, we assert p(i, j, n) when the cell in row i and column j has the given value n.
We assert that every row contains every number:
$$\bigwedge_{i=1}^{9} \bigwedge_{n=1}^{9} \bigvee_{j=1}^{9}~p(i,j,n)$$
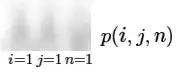
i=1 j=1 n=1stays (as in your comment) and alsop(i,j,n)stay this way (as I wrote here, not like in your comment)? Now how to change everything other so that it is equal to the proposition in my question? – vasili111 Aug 24 '18 at 15:32