18

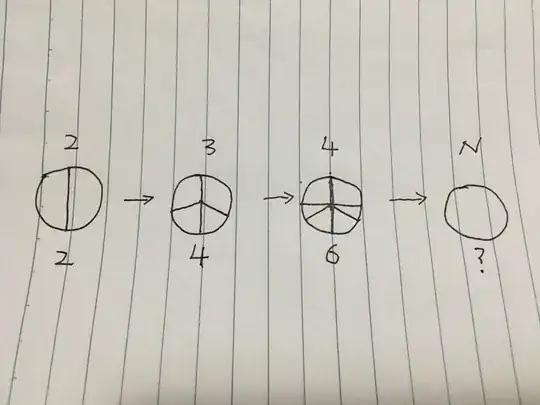
At the beginning, we had a whole piece of pizza and two people. So we cut the pizza into two slices of the same size. But at the same time, there is another guy joined us. We had to re-cut the pizza into three parts of the same size. This time we only need to cut two more times. But this was not the end yet, people were keep coming one by one. Every time we divided the pizza into equals with a minimum times of cut.$^{1}$ In the end, a total of N people came. How many slices of pizza do we have? Is there a way to figure it out quickly?

$^{1}$ The slices cannot be rearranged to get a smaller number of cuts. We cut the pizza in place, at $n$ equally-placed lines, as in the image below.

Demonstration

Caleb Stanford
  • 47,093
crazyjin
  • 183
  • 3
    You may benefit from studying our guide to new askers. It would be better if you included either your own thoughts, or possibly the origin of this problem? Also the rules are a bit unclear. Do the extra people come one at a time? Is it ok for the share of a single guest to come from a thin slice here, another there, or do they need to get a contiguous slice of $1/n$th of the pizza? – Jyrki Lahtonen Aug 21 '18 at 19:35
  • What if I tilt the pizza ever so slightly before making any cuts? Then I can increase the number of pieces at each stage. To avoid this ambiguity it seems sensible to define the cuts at the $n$-th roots of unity in the complex plane give how you're drawn them so far. – CyclotomicField Aug 21 '18 at 19:35
  • Also, this rings a bell. Did you search the site? – Jyrki Lahtonen Aug 21 '18 at 19:35
  • It's like $2N-1$ pieces. – delusional.existence Aug 21 '18 at 19:38
  • I don't think it will be easy. After four people you have two each of $\frac 14, \frac 16, \frac 1{12}$. When the fifth person comes, clearly you take $\frac 1{20}$ off each $\frac 14$. You can finish by cutting $\frac 1{60}$ off each sixth, for ten pieces. This is sufficient for both $5$ and $6$ people. There are other ways to do $5$ which may be better or worse later on. I didn't find anything that struck me for $2,4,6,10,10$ in OEIS – Ross Millikan Aug 21 '18 at 19:38
  • Are you allowed to rearrange the pieces? In the image you seem to just do them at equally-spaced intervals. In Ross Millikan's interpretation you try to rearrange them to make the minimum number of new cuts each time a new person comes. – Caleb Stanford Aug 21 '18 at 20:00
  • @6005 No rearrangement. – crazyjin Aug 21 '18 at 20:02
  • Even with rearrangement the cut for $5$ does not satisfy $6$, so for $6$ there have to be $12$ pieces. There are many more sequences with $2,4,6,10,12$ in OEIS but none looked right. – Ross Millikan Aug 21 '18 at 20:07
  • what is considered a cut? for 4 people I think it should be 5 cuts, not 6 as we get the required arrangement just by cutting once across the diameter – Vasili Aug 21 '18 at 20:09
  • 1
    Cuts look related to the Farey sequence, confirmed by the solutions posted – Mark Bennet Aug 21 '18 at 20:15
  • Looks like there are at least 3 interpretations of the problem in the comments, indicating the question would have benefitted from clearer formulation. I hope my edit is the correct clarification. – Caleb Stanford Aug 21 '18 at 20:17
  • @JyrkiLahtonen No, I did not. It's my first question about math. I did not know this is such a serious place. Sorry about this. – crazyjin Aug 21 '18 at 22:55
  • The edit did made it clearer. Retracting my vote to put this on hold. – Jyrki Lahtonen Aug 22 '18 at 05:13
  • See also https://math.stackexchange.com/questions/1383406/minimum-cake-cutting-for-a-party/ and the other questions linked there. – Gerry Myerson Nov 20 '23 at 01:59

2 Answers2

9

We may identify angles for the slices with real numbers between $0$ and $1$. At step $n$, we cut at angles $0, \frac{1}{n}, \frac{2}{n}, \ldots, \frac{n-1}{n}$. (As clarified in the comments, the problem seems to assume this. Note that there is a more interesting question if we are allowed to rearrange the pieces, or if we are allowed to place the cuts at any arbitrary angle as long as the lines are equally spaced.)

Thus, the number of slices after $n$ people have joined is equal to the number of rational numbers in the interval $[0,1)$ with denominator at most $n$. The number with denominator exactly $k$ is $\phi(k)$, where $\phi$ is the totient function which counts how many numbers between $0$ and $k-1$ (numerators) are relatively prime to the $k$ (the denominator).

Therefore, the total number of slices after $n$ people have joined can also be expressed as $$ a_n = \sum_{k=1}^n \phi(k). $$

The sequence $a_n$ begins $2, 4, 6, 10$ as in your picture. More information on the sequence can be found in this Online Encyclopedia of Integer Sequences page.

Caleb Stanford
  • 47,093
  • This problem comes from no where but boring. I know almost nothing about the numbers. It's amazing that you can find the solution in such a short time. I checked a few numbers in the sequence and they are all correct. I don't have enough knowledge to verify the function you gave. But I will write a small program to verify the numbers in the sequence. – crazyjin Aug 21 '18 at 21:24
  • @crazyjin It's definitely correct as it's the same answer I arrived at using a slightly different method. – CyclotomicField Aug 22 '18 at 00:01
8

First, let us consider the cuts to be the $n$-th roots of unity in the complex plane and let $\phi(n)$ be Euler's totient function. I claim that the number of cuts is $\sum_{k=1}^n\phi(k)$. To see this first we note that for some prime $p$ the only divisor is $1$ we must make $p-1$ new cuts since those roots of unity could not be cut yet or it would imply a divisor of $p$. Now for some composite $n$ as we traverse the circle by taking multiples of $e^{2\pi i/n}$ then we note that for some cut $e^{2 \pi i k/n}$ to have already been made implies that $k$ divides $n$. This means we will make a new cut when $k$ is relatively prime to $n$. Summing over these cuts for each $n$ gives us the result.

CyclotomicField
  • 11,925
  • 1
  • 14
  • 32