24

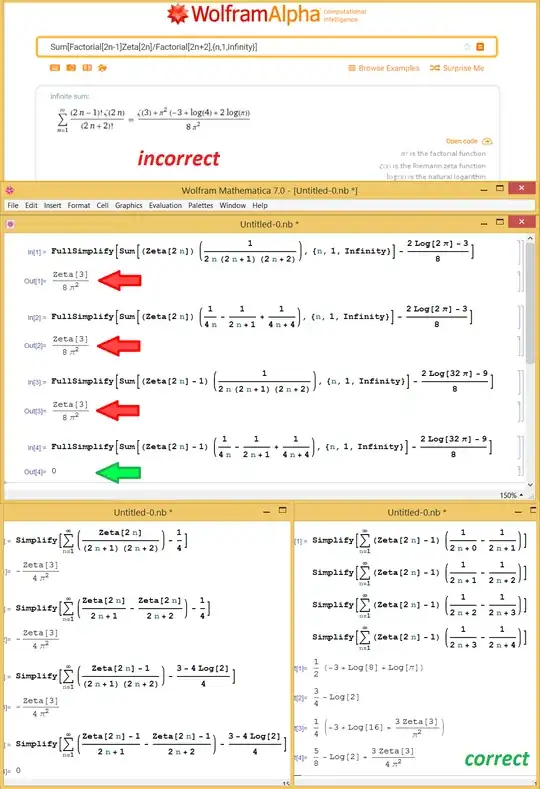
From a mathematical point of view, what phenomena that most likely Mathematica Wolfram encountered when calculating: $$ \sum_{n=1}^{\infty}\frac{(2n-1)!}{(2n+2)!}\zeta(2n)\,=\,\color{red}{\frac{2\log(2\pi)-3}{8}+\frac{\zeta(3)}{8\pi^2}} $$ which is incorrect.

While calculating the sum from this question, I noticed that Wolfram result is containing ${\small\,\frac{\zeta(3)}{8\pi^2}\,}$, which is incorrect. Although I realized that this could be a bug, I started to wonder if there are any logical explanation behind this miscalculation! Has Wolfram algorithm encountered something similar to Riemann Rearrangement Theorem?

Doing more investigations, it turns-out that Wolfram is incorrectly miscalculating the closed form of an entire class of zeta summation, except the last case which is correct. $$ \small \begin{align} \sum_{n=1}^{\infty}\frac{\zeta(\alpha\,n)}{(n+a)(n+b)\dots} &= \sum_{n=1}^{\infty}\left[A\frac{\zeta(\alpha\,n)}{n+a}+B\frac{\zeta(\alpha\,n)}{n+b}+\dots\right] = \\ C+\,\sum_{n=1}^{\infty}\frac{\zeta(\alpha\,n)-1}{(n+a)(n+b)\dots} &= \color{darkgreen}{\sum_{n=1}^{\infty}\left[A\frac{\zeta(\alpha\,n)-1}{n+a}+B\frac{\zeta(\alpha\,n)-1}{n+b}+\dots\right]\,+C} \end{align} $$ And with the appearance of this case (the last correct closed form), I believe there is a mathematical explanation regarding a correct summation method or algorithm that gives a kind of systematic incorrect closed form if it applied in a certain way. Appreciating if someone can explore this and alert us regardless of any bug that may exist in any math app. Thanks.

enter image description here

Community
  • 1
Hazem Orabi
  • 4,570
  • 2
  • 17
  • 38
  • 2
    Quite difficult to say what is really happening there. In my experience with old versions of Mathematica, I have seen $\text{NIntegrate}$ and $\text{N[Integrate]}$ yielding radically different outputs when dealing with elliptic integrals and the like. A non-legit rearrangement of some sort is likely. – Jack D'Aurizio Aug 14 '18 at 13:16
  • 1
    Or maybe a bad management of the branches of the complex logarithm, or maybe... what happens if we compute such series through Euler-Maclaurin, and completely ignore the integral error term? – Jack D'Aurizio Aug 14 '18 at 13:21
  • 8
    Or maybe it is just an intended lesson: don't trust the machines too much. – Jack D'Aurizio Aug 14 '18 at 13:21
  • 1
    @JackD'Aurizio : The deference between the correct and incorrect answer is the term ${,\frac{\zeta(3)}{8\pi^2},}$, I am wondering how to re-arrange the summation to generate such term. – Hazem Orabi Aug 14 '18 at 13:53
  • 2
    It might be related to the factorial. Because if we put the gamma function instead its evaluated correctly. link – Zacky Aug 14 '18 at 16:16
  • @Zacky : Nice observation! Being more precise, we have to change both factorials from nominator and denominator ${\small\displaystyle\sum_{n=1}^{\infty}\frac{\Gamma(2n)}{\Gamma(2n+3)}\zeta(2n)}$. Most probably Wolfram is starting now by simplifying ${\small\displaystyle\frac{\Gamma(2n)}{\Gamma(2n+3)}=\frac{1}{(2n)(2n+1)(2n+2)}}$. Okay, at least we now know that we shouldn’t start by this simplification. – Hazem Orabi Aug 14 '18 at 18:13
  • The sum behavior, ${\small\displaystyle\frac{1}{(2n)(2n+1)(2n+2)}\sim\frac{1}{n^3}}$, explains somehow the appearance of the term ${\small\displaystyle\zeta(3)}$. – Hazem Orabi Aug 14 '18 at 18:15
  • Also note that $\frac{1}{(2n)(2n+1)(2n+2)} = 1/(4 (n + 1)) - 1/(2 n + 1) + 1/(4 n)$. – marty cohen Aug 15 '18 at 00:00
  • I know that \displaystyle often "looks better", but it should be avoided in the tilte. – Asaf Karagila Aug 15 '18 at 15:05

1 Answers1

6

Only a note.

WolframAlpha can calculate Sum[Zeta[2n]*(2n-1)!/(2n+1)!, {n,1,Infinity}]

$\displaystyle \left(=\sum\limits_{n=1}^\infty \frac{\zeta(2n)(2n-1)!}{(2n+1)!}\right)\enspace$ exactly

but can only approximate Sum[Zeta[2n]*(2n)!/(2n+2)!, {n,1,Infinity}]

$\displaystyle \left(=\sum\limits_{n=1}^\infty \frac{\zeta(2n)(2n)!}{(2n+2)!}\right)$.

This is indeed strange, because the difficulty is about the same. WolframAlpha has problems with slow converging series.

Maybe the term $\,\,\text{$\zeta(3)/(8\pi^2$)}\,\,$ is by chance, because the calculation inaccuracy seems to be very close to this term at some point of the calculations.

It's interesting, that WolframAlpha calculates

Sum[Zeta[2n](2n-1)!/(2n+3)!, {n,1,Infinity}]$~\displaystyle \left(=\sum\limits_{n=1}^\infty \frac{\zeta(2n)(2n-1)!}{(2n+3)!}\right)$

exactly including $\,\text{$\zeta(3)/(8\pi^2$)}$, here $\,\text{$9\zeta(3)/(72\pi^2$)}\,$ .

pshmath0
  • 11,208
user90369
  • 11,696