How to get the angle of the figure?

Question

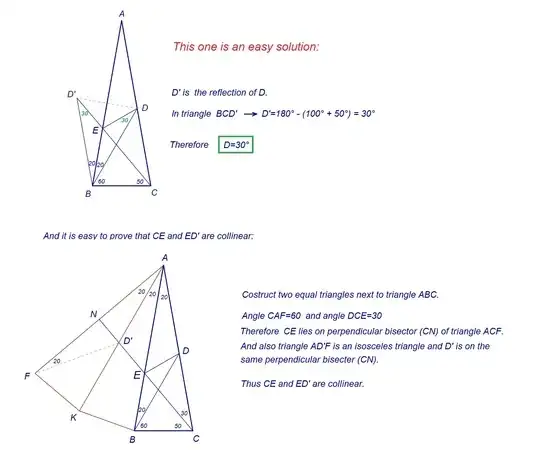
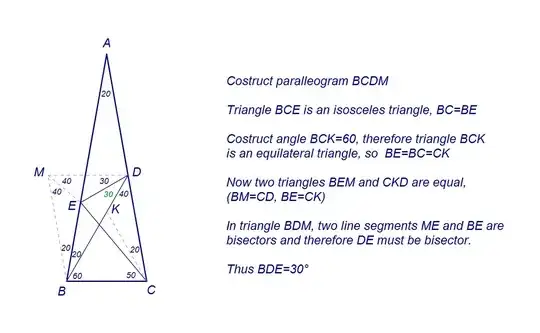
I have this problem, that can be solved with elemental knowledge.

In order to challenge, I can't draw extra segments to solved it.

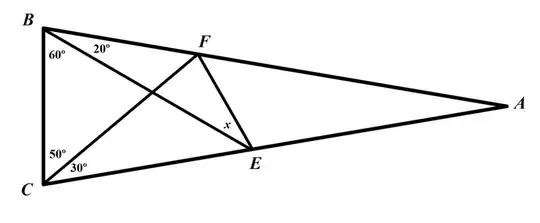
This is the problem and i need to get the measure of $\angle{x}$

My current development is:

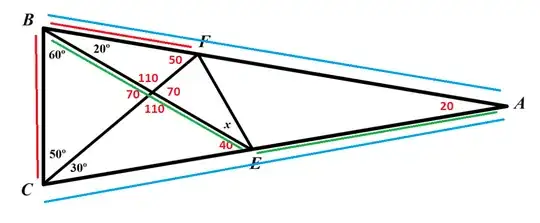
Well, the sides with equal colour are congruent, and I have completed all the angles that I could, in red colour.

Then, how i can get the $\angle{x}$ in a elementary form, without draw extra segments? Is possible ?

Introducing another variable for one of the angles you haven't solved for may help. Try to write two angles in two different ways using your variables. This will give you a system of two linear equations in two variables. — Dzoooks, Aug 06 '18 at 15:49

score 1 · Answer 1 · answered Aug 06 '18 at 16:13

By the sine rule $$green/red = \sin80/\sin40 = 2\cos40$$ and also $$green/red = \sin(160 - x)/\sin x = \sin(20 + x)/\sin x = \sin20\cot x + \cos 20$$ Therefore $$\sin20\cot x = 2\cos40 - \cos20 = \cos40 - 2\sin30\sin10 = \sin50 - \sin10 = 2\sin20\cos30$$ so $\cot x = 2\cos30 = \sqrt3$ and $x = 30$ degrees.

Michael Rozenberg · Answer 2 · 2018-08-06T16:36:42.927

I think, we can get a solution without drawing of an extra segments by trigonometry only.

The geometric solution:

Let $D\in FA$ such that $DE||BC$ and $DC\cap BE=\{G\}$.

Thus, $\Delta BGC$ and $\Delta DGE$ they are equilaterals and since $$\measuredangle BFC=\measuredangle FCB=50^{\circ},$$ we obtain: $$FB=BC=BG,$$ which says that $$\measuredangle FGB=\frac{180^{\circ}-20^{\circ}}{2}=80^{\circ},$$ which gives $$\measuredangle FGE=100^{\circ}.$$ But also $\measuredangle FDE=100^{\circ}$ and $DE=EG$.

Thus, $\Delta DEF\cong\Delta GEF,$ which says $$\measuredangle FEB=\frac{1}{2}\measuredangle DEG=30^{\circ}.$$