0

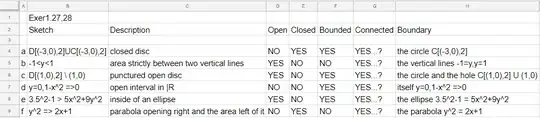
A First Course in Complex Analysis by Matthias Beck, Gerald Marchesi, Dennis Pixton, and Lucas Sabalka Exer 1.27,8

enter image description here

Here are my answers:

enter image description here

  1. Where have I gone wrong?
  2. About connected, my topology is so far limited to the elementary topology in elementary analysis, complex analysis and real analysis, how exactly do we prove those sets are connected? Suppose they're not connected and then derive a contradiction like in my other question Elementary topology of $\mathbb C$: Union of 2 regions with nonempty intersection is a region ?
  3. Is there a way to check this using computers? Not sure I can use Wolfram Alpha or guess I don't know how. Are there programs for this? Like can I do this in Matlab, scilab or R?
BCLC
  • 14,197
  • 3
    Why do you think (a) describes a closed disk? – xbh Jul 30 '18 at 10:39
  • @xbh Re(a): No idea. Been weeks since I did this and am just revising now. I get that it's open. Thanks! – BCLC Jul 30 '18 at 12:16
  • 1
    Glad to help. Maybe you just get exhausted and did not notice this. It's fine. For mathematical softwares, WolframAlpha is applicable [like drawing the graph of sets], but those properties needs to be verified by you. – xbh Jul 30 '18 at 12:32
  • 1
    And yes, path connectedness implies connectedness. The former one seems much more acceptable from our intuition. – xbh Jul 30 '18 at 12:34
  • 1
    Why down vote…? – xbh Jul 31 '18 at 02:47
  • @xbh Probably a user who's been serially downvoting me since 2015. This may or may not have led the user to have been suspended during hats in Dec 2015. – BCLC Jul 31 '18 at 03:33

1 Answers1

1

a) Wrong. It's the open disk $D(-3,2)$. In particular, it is open and it is not closed.

b) Right.

c) Right, but you should write $1$ instead of $(1,0)$.

d) Right, except that it is closed.

e) Right.

f) Right.

For each set, the easiest way to prove that it is connected consists in proving that it is path-connected.

José Carlos Santos
  • 440,053
  • Thanks, José Carlos Santos! Re(a): No idea why I thought closed disc. Been weeks since I did this and am just revising now. I get that it's open. Re connected: Oh like in Thm 1.12 ('If any two points in G ⊆ C can be connected by a path in G, then G is connected')? Re computers: Any suggestions please? – BCLC Jul 30 '18 at 12:17
  • Re path connected: How would you go about proving they are path connected please? For a,b,d,e: I guess we can say for path connected that we can draw a line between any 2 points s.t. the line is still in the set ('convex' isn't introduced in Ch1). What about c and f? Hmmm...perhaps respectively semi-circle and parabola instead of line if line fails? – BCLC Jul 30 '18 at 12:30
  • 2
    @BCLC Yeah, that's the gist. For c) try an arc and a line segment. For f) use parabola and a line segment. – xbh Jul 30 '18 at 13:25
  • @xbh Oh right arc not semi-circle. Anyhoo, why 'and a line' or 'or a line' ? – BCLC Jul 30 '18 at 21:49
  • 1
    @BCLC Sorry for my non-rigorous expression. I mean a line segment. – xbh Jul 31 '18 at 01:45
  • @xbh oh wait mistake I meant 'and not' instead of 'or'. Anyhoo for c and f, sometimes a line segment alone will work otherwise we may use an arc of a circle or parabola either by itself or along with a line segment. Right? – BCLC Jul 31 '18 at 02:05
  • 1
    @BCLC Right. An arc of a circle along with a line segment always works in c). Similar thing for f). – xbh Jul 31 '18 at 02:47
  • @xbh Thanks! You could post as answer if you want – BCLC Jul 31 '18 at 03:34