2

Where can I find the identities of Ramanujan concerning the Floor Function with its solution? Any site you can recomend to me? 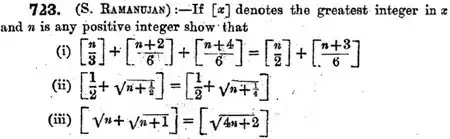enter image description here

user573497
  • 311

2 Answers2

3

For (i), write $n=6k+r$ where $r\in \{0,1,...,5\}$. Then left side is $$\begin{eqnarray}\Big[{n\over 3}\Big]+ \Big[{n+2\over 6}\Big]+\Big[{n+4\over 6}\Big] &= &\Big[{6k+r\over 3}\Big]+ \Big[{6k+r+2\over 6}\Big]+\Big[{6k+r+4\over 6}\Big]\\ &= &2k+\Big[{r\over 3}\Big]+ k+\Big[{r+2\over 6}\Big]+k+\Big[{r+4\over 6}\Big]\\ &= &4k+\underbrace{\Big[{r\over 3}\Big]+\Big[{r+2\over 6}\Big]+\Big[{r+4\over 6}\Big]}_{E_r}\\ \end{eqnarray}$$ $$E_r=\left\{% \begin{array}{ll} 0, & r=0,1\\ 1, & r=2 \\ 2, & r=3 \\ 3, & r=4,5 \\ \end{array}% \right.$$ And the right side is $$\begin{eqnarray}\Big[{n\over 2}\Big]+ \Big[{n+3\over 6}\Big]&= &\Big[{6k+r\over 2}\Big]+ \Big[{6k+r+3\over 6}\Big]\\ &= &3k+\Big[{r\over 2}\Big]+ k+\Big[{r+3\over 6}\Big]\\ &= &4k+\underbrace{\Big[{r\over 2}\Big]+\Big[{r+3\over 6}\Big]}_{F_r}\\ \end{eqnarray}$$ $$F_r=\left\{% \begin{array}{ll} 0, & r=0,1\\ 1, & r=2 \\ 2, & r=3 \\ 3, & r=4,5 \\ \end{array}% \right.$$ So both sides are the same for all $r$ and we are done.

nonuser
  • 91,557
  • Why did you just let $n=6k+r$? Is this the general form of an positive integer? – user573497 Jul 28 '18 at 15:56
  • That is correct. If we had $[n/11]$ then I would write $n=11k+r$ and $0\leq r\leq 10$ – nonuser Jul 28 '18 at 16:08
  • 1
    oh, I get it! You did that for convenience since in the denominator there is a $6$. If it were some arbitrary number un the denominator like $m$, then I consider the integer $n=mk+r$ where 0\leqr\ls – user573497 Jul 28 '18 at 16:33
  • 1
    Sorry, I couldn't edit the last comment. I tried to say that $n=mk+r$ where $r$ is an integer between $0$ and $m-1$. – user573497 Jul 28 '18 at 16:36
  • I can understand now! Thanks for the feedback! :) – user573497 Jul 28 '18 at 16:38
0

If $[x]$ denotes floor we have $$\sum\limits_{k=0}^{m-1}\Big[{n+ks+t\over ms}\Big]=\Big[{n+t\over s}\Big]$$ for $n\geqslant0$, $m>0$, $s>t\geqslant0$, $n,m,s,t$ - integers. So $$\Big[{n\over 2}\Big]=\Big[{n\over 6}\Big]+\Big[{n+2\over 6}\Big]+\Big[{n+4\over 6}\Big]$$ $$\Big[{n\over 3}\Big]=\Big[{n\over 6}\Big]+\Big[{n+3\over 6}\Big]$$ and obviously $$\Big[{n\over 3}\Big]+\Big[{n+2\over 6}\Big]+\Big[{n+4\over 6}\Big]=\Big[{n\over 2}\Big]+\Big[{n+3\over 6}\Big]$$ With same conditions for $n,m,s,t$ if $[x]$ denotes ceiling we have $$\Big[{n\over 3}\Big]+\Big[{n+2\over 6}\Big]+\Big[{n+4\over 6}\Big]=\Big[{n+2\over 2}\Big]+\Big[{n+3\over 6}\Big]$$ and also if $[x]$ denotes nearest integer we have $$\Big[{n+2\over 3}\Big]+\Big[{n+2\over 6}\Big]+\Big[{n+4\over 6}\Big]=\Big[{n+2\over 2}\Big]+\Big[{n+3\over 6}\Big]$$

user514787
  • 1,473