2

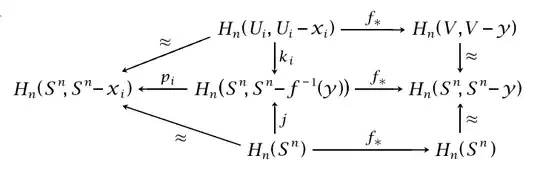
In Hatcher's Algebraic Topology, he gives a formula for computing the degree of a map $f_*: H_n(S^n) \to H_n(S^n)$ in case some point $y$ in $S^n$ has preimage consisting only of finitely many points $x_i$. Then $\deg f = \sum_i \deg f \mid_{x_i}$. enter image description here

He uses the above diagram to illustrate the proof. Let $U_i$ be disjoint neighbourhoods of the $x_i$. Then by excision, he writes, the central term $H_n(S^n, S^n - f^{-1}(y))$ is the direct sum of the groups $H_n(U_i, U_i - x_i) \cong \mathbb Z$.

Now I think this is what he means: The interior of $\bigcup_i U_i \,\cup (S^n - f^{-1}(y))$ covers $S^n$ so we can apply the excision theorem. Since the $U_i$ are all disjoint, we get an isomorphism $\bigoplus_i H_n(U_i, U_i - x_i) \cong H_n(S^n, S^n - f^{-1}(y))$.

I would like to know whether I'm on the right track here.

Apart from this, I would like to gain some geometric intuition as to why the $n$-th homology group of the $n$-sphere relative to the $n$-sphere with $k$ points removed is $\bigoplus_{i=1}^k \mathbb Z$. Since $(S^n, S^n - f^{-1}(y))$ is not what Hatcher calls a good pair we are technically not allowed to think in terms of $S^n/(S^n - f^{-1}(y))$. I've tried that anyway but it didn't help.

Considering the special case of $H_1(S^1 / S^1 - \{x_1, x_2, x_3\})$, we see that the elements of this homology group are generated by paths in $S^1$ with endpoints not in $\{x_1, x_2, x_3\}$. I can't see intuitively how this gives $H_1 \cong \mathbb Z \oplus \mathbb Z \oplus \mathbb Z$ and I would appreciate any help.

bsbb4
  • 3,751
  • 1
    One way to understand the relative homology $H_*(S^n,S^n-f^{-1}(y))$ is by Alexander duality, as discussed by Hatcher around Th. 3.44 and Co, 3.45. – Tyrone Jul 27 '18 at 12:31

1 Answers1

2

You excise the set $B = S^n - \bigcup_{i=1}^k U_i$. This is possible because $B$ is closed and contained in $S^n - f^{-1}(y)$ which is open. Therefore

$$H_n(S^n,S^n - f^{-1}(y)) \approx H_n(\bigcup_{i=1}^k U_i, \bigcup_{i=1}^k (U_i - x_i)) = H_n(\bigcup_{i=1}^k( U_i, U_i - x_i)) \approx \bigoplus_{i=1}^k H_n(U_i, U_i - x_i) .$$

An element of $H_n(S^n,S^n - f^{-1}(y))$ is a homology class of a chain of singular $n$-simplices in $S^n$ whose boundary is contained in $S^n - f^{-1}(y)$. The most elementary such chains are single $n$-simplices in $S^n$ which contain exactly one $x_i$ in its interior. It can be shown that they generate the complete relative homology group. I am not sure whether this fact is intuitively clear, but the purpose of homology theory is to give a formal framework.

Paul Frost
  • 87,968