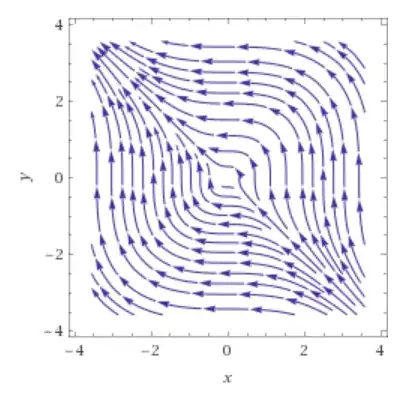
Make the qualitative study of the ODE on the plane $$ \begin{cases}\dot x = - y^2\\ \dot y= x^2 \end{cases} $$ and determine how many solutions satisfy $y(0) = x(1) = 0$.
My attempt.
Let $f(x,y):=\begin{pmatrix}-y^2\\x^2 \end{pmatrix}$ be the vectorial field. It is well defined on all plane and $C^1$, then every Cauchy Problem has a unique local solution and every one of these solution can be extended in unique way to a maximal solution (not necessary globally defined). Now I note that the function $$E(x,y):=\frac{x^3}{3}+\frac{y^3}{3}$$ is a constant of motion, i.e. $\dot E(x(t),y(t))=c$, where $(x(t),y(t))$ is a solution. The orbits are the level sets of $E$, that are open curves like this: https://m.wolframalpha.com/input/?i=plot+x%5E3+%2B+y%5E3+%3D+10, or https://m.wolframalpha.com/input/?i=plot+x%5E3+%2B+y%5E3+%3D+-10.
It is all correct?
Do you think that it is enough ? The task "Make the qualitative study" is very generic. What would you add?
I don't know how to determine how many solutions satisfy $y(0) = x(1) = 0$.