How do I place the poles and zeros form a disired system? Adaptive control

Question

If I have a transfer function of a system $G(s)$

$$G(s) = \frac{4 - 2s}{4 + 0.8s + s^2}$$

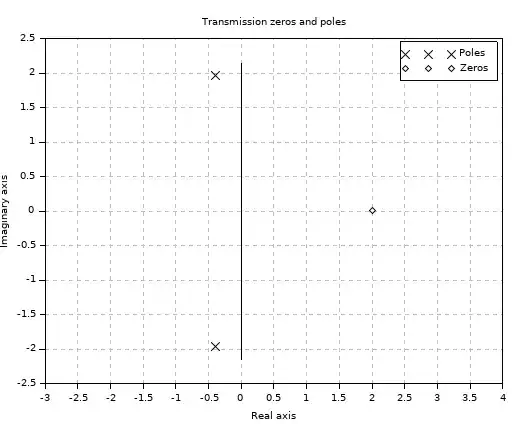
$G(s)$ has the poles and zeros and is a stable system.

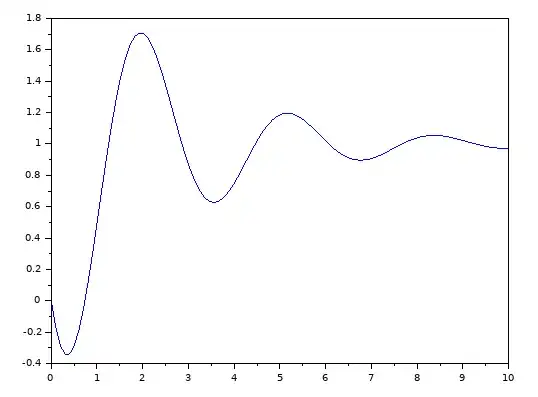
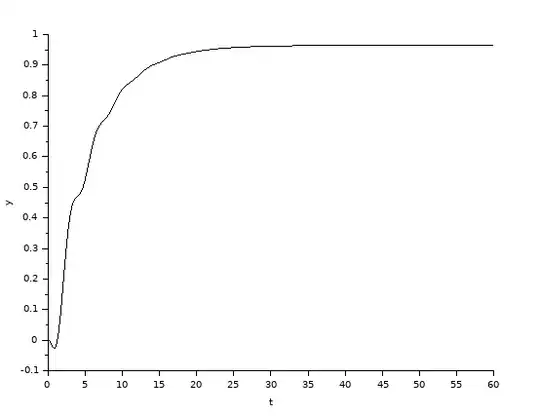
And the step answer look like. It has a delay as you can see, a.k.a non-minimum phase system.

I want to control the system $G(s)$ so it will act as the system $G_m(s)$

$$G_m(s) = \frac{\omega^2}{ s^2 + 2\eta \omega s + \omega ^2} = \frac{1}{1 + 1.4s + s^2 }$$

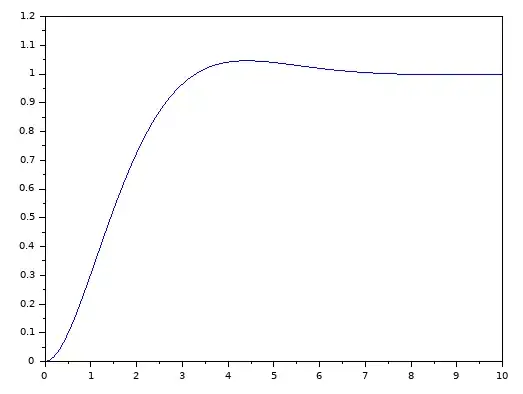
Where $\eta = 0.7$ and $\omega = 1$. The step answer look like:

The first thing I need to to is to turn both $G_m(s)$ and $G(s)$ to discrete transfer functions with the sampling rate of $h=0.1$.

$$H_m(s) = \frac{B_m}{A_m} = \frac{b_{m0} z + b_{m1}}{a_{m0} z^2 + a_{m0} z + a_{m1}} = \frac{0.0045531 + 0.0047707z }{0.8693582 - 1.8600345z + z^2 }$$

$$H(s) = \frac{B}{A} = \frac{b_0 z + b_1}{az^2 + a_0 z + a_1} = \frac{0.2098316 - 0.1715178z }{0.9231163 - 1.8848025z + z^2}$$

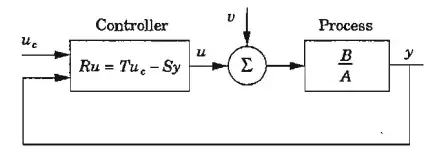
We follow this feedback system:

Where $R, T, S$ are polynomials and $u_c$ is reference input and $y$ is output and $v$ is disturbance input.

The control law $$u = \frac{T}{R}u_c - \frac{S}{R}y$$

Will result the closed loop system:

$$y =\frac{BT}{AR + BS}u_c + \frac{BR}{AR + BS}v$$

Let's say that $v = 0$ and we only focusing on:

$$y =\frac{BT}{AR + BS}u_c$$

Our goal is that the system model $H_m$ should have the same behaviour as reference model $H_m$

$$y =\frac{BT}{AR + BS}u_c = \frac{B_m}{A_m}u_c$$

That means we can write down the diophantine equations:

$$BT = B_m$$ $$AR + BS = A_m$$

Which can be solved as:

$$T = \frac{B_m}{B} = \frac{b_{m0} z + b_{m1}}{b_0 z + b_1}$$

And if we assume $R = 1$ when we can say:

$$S = \frac{A_m - A}{B} = \frac{(a_m - a)z^2 + (a_{m0} - a_0) z + (a_{m1} - a_1)}{b_0 z + b_1}$$

In all cases, $$(a_m - a)z^2= 0$$ so $S$ will be:

$$S = \frac{A_m - A}{B} = \frac{(a_{m0} - a_0) z + (a_{m1} - a_1)}{b_0 z + b_1}$$

Question:

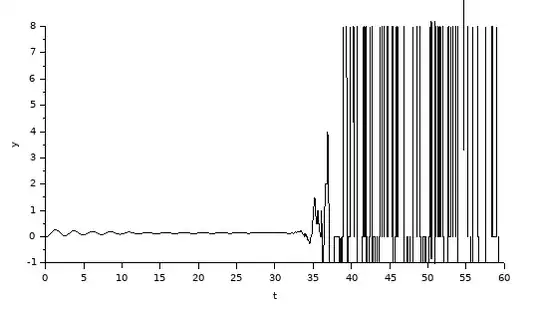
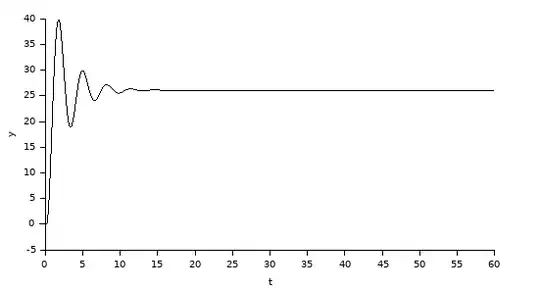
This will work, if the $G(s)$ system has no positive zeros. Rigth now, it has one zero at 2. When I simulate the system, it look like this:

How can I find the polynomals $T, R, S$ so the model $G(s)$ can follow $G_m(s)$ ?

Hint:

If you use Recursive Least Square(RLS) to estimate $b_0, b_1, a_0, a_1$, then you have a self tuning controller.

EDIT:

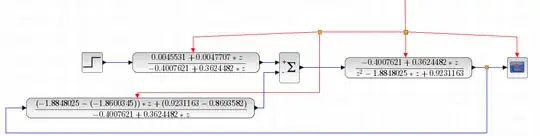
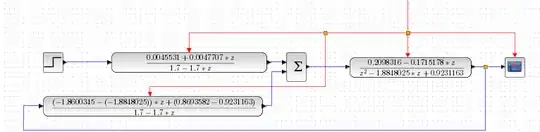
I tried this:

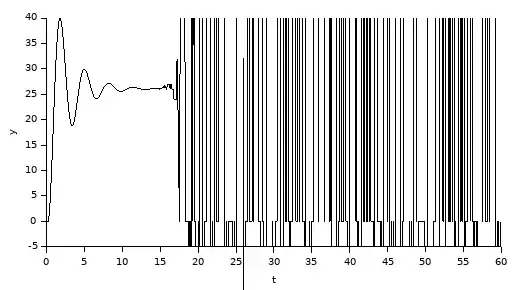
And the result was:

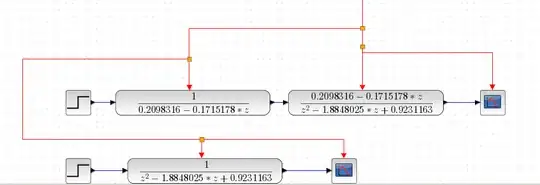
The system above:

The system below:

Clearly I can se that the $z$ variable is out of the unit circle = unstable system:

$$1.2233809 = \frac{0.2098316}{0.1715178}$$

So $T, S$ are unstable transfer functions. How can I make them stable?

Answer 1

I found a answer now!

In this case $B$ was $b_0 z + b_1$.

I set

$$b_0 = - |\frac{A_m(1)}{B(1)} + 0.01|= -|\frac{0.8693582−1.8600345*1+1^2}{0.2098316−0.1715178*1} + 0.01| -1.71$$

And $$b_1 = |\frac{A_m(1)}{B(1)}| = |\frac{0.8693582−1.8600345*1+1^2}{0.2098316−0.1715178*1}| = 1.71$$

The constant of 0.01 is just so the denominator don't having an integration effect.

And the result was:

One issue left is the reference tracking factor. Right now the step answer is -3 and the $y$ is 0.95. I need a reference tracking. Do you know how to create one? It's need to be an adaptive one!