0

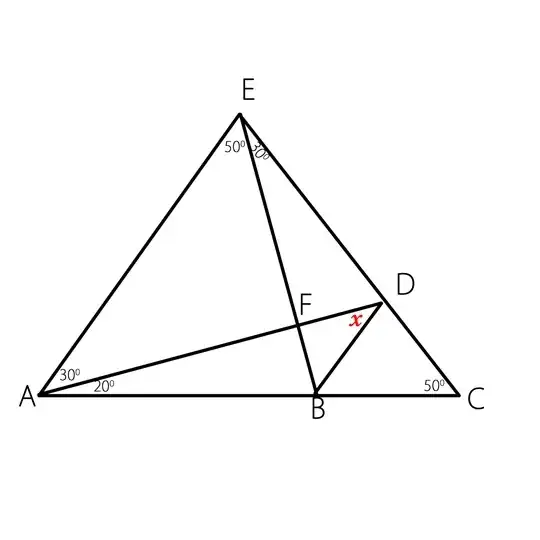
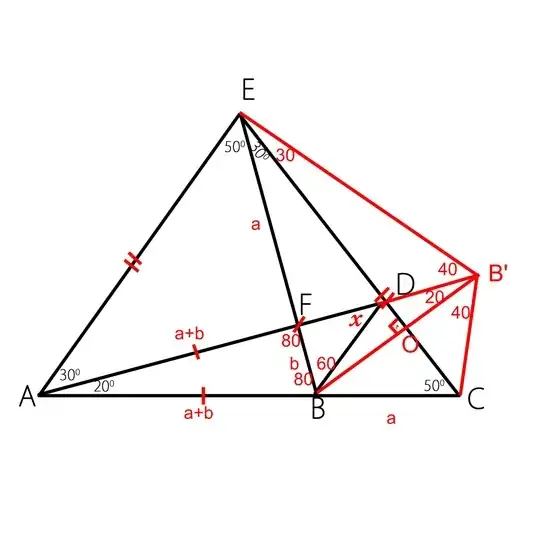
enter image description here

I have to find the value of $x$ and I did it and found out $x=40^0$. I used the cot theorem to find it. but without trigonometry is there a purely geometric proof? every single time I tried I was stopped at $x+F\hat BD=80^0$. Any hint or a proof would be appreciated.

P.S this is different from Langley’s Adventitious Angles problem since $CE \neq AC$ I saw some basic constructions led me to have some cyclic quadrilaterals. but they also did not gave me the answer

thomson
  • 667
  • @fleablood But someone told me that this can be proved with only using elementary construction, cyclic quadrilateral, and similar triangles. – thomson Jun 19 '18 at 08:40
  • The question has been asked (and answered) here several times. Search here, or on the web, for "adventitious angles". For example, https://math.stackexchange.com/questions/548292/determinating-the-angle-in-a-triangle and https://math.stackexchange.com/questions/6942/finding-an-angle-within-an-80-80-20-isosceles-triangle – Gerry Myerson Jun 19 '18 at 09:12
  • 1
    Possible duplicate of Finding an angle within an 80-80-20 isosceles triangle – Gerry Myerson Jun 19 '18 at 09:14
  • Perhaps there's some manipulation of angles. Afterall you have 30 which is half of sixty. But it's not obvious. Why not use trig. They teach the trig definitions and law of sines/cosines in most geometry classes these days. – fleablood Jun 19 '18 at 16:50

2 Answers2

3

In this picture, there are some things that have to be further explained:

First of all, we take the symmetry of $\Delta BEC$. Then we draw a line from $B$ to $B'$ in order to have an equilateral triangle $\Delta BEB'$. Then we have the equality $|EB| = |BB'| = |EB'| = |AB|$. Here, since $\angle EBB' = 60^\circ$ and $|AB| = |BB'|$, we can conclude that $A$, $F$, $D$ and $B'$ are linear and $\angle AB'B = 20^\circ$. Then by noticing the fact that $EO$ is median of the equilateral triangle, it is median of $\Delta BDB'$ as well, which implies that $\angle DBB' = 20^\circ$. Therefore $x = 40^\circ$.

enter image description here

ArsenBerk
  • 13,388
0

Easy to see that $$\measuredangle DBC=20^{\circ}+x$$ and $$\measuredangle EBD=80^{\circ}-x.$$ Thus, by law of sines we obtain: $$\frac{ED}{DC}=\frac{\frac{ED}{BD}}{\frac{DC}{BD}}=\frac{\frac{\sin(80^{\circ}-x)}{\sin30^{\circ}}}{\frac{\sin(20^{\circ}+x)}{\sin50^{\circ}}}=\frac{2\sin(80^{\circ}-x)\sin50^{\circ}}{\sin(20^{\circ}+x)}.$$ In another hand, $$\frac{ED}{DC}=\frac{\frac{ED}{AD}}{\frac{DC}{AD}}=\frac{\frac{\sin30^{\circ}}{\sin80^{\circ}}}{\frac{\sin20^{\circ}}{\sin50^{\circ}}}=\frac{\sin50^{\circ}}{2\sin80^{\circ}\sin20^{\circ}}.$$ Thus, $$4\sin20^{\circ}\sin80^{\circ}\sin(80^{\circ}-x)=\sin(20^{\circ}+x)$$ or $$2(\cos60^{\circ}-\cos100^{\circ})\sin(80^{\circ}-x)=\sin(20^{\circ}+x)$$ or $$\sin(80^{\circ}-x)+\sin(160^{\circ}-x)-\sin{x}=\sin(20^{\circ}+x)$$ or $$\sin(80^{\circ}-x)=\sin{x},$$ which gives $$x=40^{\circ}.$$

Michael Rozenberg
  • 203,855