An approximate solution to an ODE

Question

I am interested in the ODE:

$x^\prime = x^2 + t^2$

$x(0)=0$

The power-series method is not (easily?) applicable here. Do you have any suggestions how to solve it?

Answer 1

It is easier to get a polynomial approximation if instead of "plug, expand, equate coefficients" we use the Picard iteration. The Picard iteration is traditionally presented as a method for proving the existence and uniqueness of solutions. But it is a constructive method, which is easy to implement for equations with polynomial right-hand side.

First, rewrite the equation in integral form: $$x(t)=\int_0^t (x(s)^2+s^2)\,ds$$ Of course we know how to integrate $s^2$: $$x(t)=\frac{t^3}{3}+\int_0^t x(s)^2\,ds$$ Now run the iteration $x_{n+1}(t) =\frac{t^3}{3}+\int_0^t x_n(s)^2\,ds$ beginning with $x_0\equiv 0$. $$x_1(t) =\frac{t^3}{3}+\int_0^t 0\,ds = \frac{t^3}{3}$$ $$x_2 (t)= \frac{t^3}{3}+\int_0^t \left(\frac{s^3}{3}\right)^2\,ds = \frac{t^3}{3}+ \frac{t^7}{3^2\cdot 7}$$ $$x_3(t) = \frac{t^3}{3}+\int_0^t \left(\frac{s^3}{3}+ \frac{s^7}{3^2\cdot 7}\right)^2\,ds = \frac{t^3}{3}+ \frac{t^7}{3^2\cdot 7}+\frac{2\,t^{11}}{3^3\cdot 7\cdot 11} + \frac{t^{15}}{3^4\cdot 7^2\cdot 15}$$ If a polynomial approximation of degree $15$ does not work for your purpose, then you probably don't want a polynomial approximation.

Answer 2

Well, the title asks for an approximate (read: numerical) solution, yet you mention attempting to find a power series solution. So I am not sure what your ultimate goal is.

Assuming the former, note that this is a stiff equation, and thus your normal set of numerical recipes won't perform well. Typically one turns to Backward Differentiation Formulas (BDF) (also known as Gear's Method), but a variety of other methods are available which you can find at the links above.

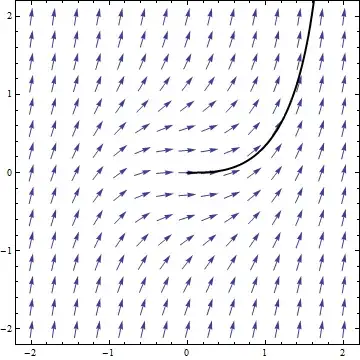
Here's a plot of such an implementation in Mathematica: