Proving that the median to the hypotenuse of a right triangle is equal to half of the hypotenuse

Question

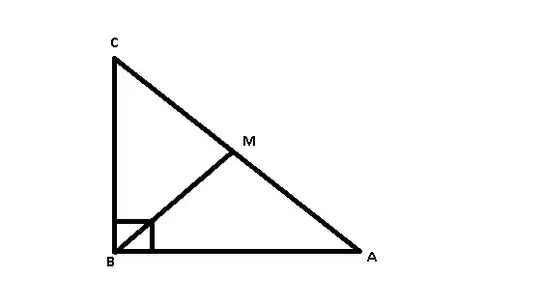
If I have a right triangle, of the form: $ABC$, with right angle at B:

Then, $BM = CM = AM$.

Then, as I show that:

$BM = AM$

The simplest demonstration is to create another triangle equal to this one, and adjust them so that it looks like a rectangle. The diagonals of a rectangle are the same, which shows the property.

But I would like to see the demonstration, without using the property of diagonals of a rectangle, in advance thanks.

The center of the circumcircle of $\triangle ABC$ is ____? – Hari Shankar Jun 13 '18 at 04:22 — Hari Shankar, Jun 13 '18 at 04:22

score 2 · Answer 1 · edited May 22 '24 at 17:09

2

Consider the circumcircle of $\triangle ABC$. Since $\angle ABC=90^{\circ}$, $AC$ is the diameter.

Thus, $M$ is the circumcenter and $MC=MB=MA$.

edited May 22 '24 at 17:09

User

8,033

answered Jun 13 '18 at 05:12

abc...

5,010

So, only in a right triangle, the circumcircle is the midpoint of hypotenuse(in this case $M$) ??? – ESCM Jun 14 '18 at 15:29

score 1 · Accepted Answer · answered Jun 13 '18 at 02:06

1

Drop the altitude from $M$ to $AB$ which will be parallel to $BC$ and find two equal right triangles.

answered Jun 13 '18 at 02:06

John McClane

1,835
9
18

To say that the right triangles are equal, you are assuming that the height falls at the midpoint of $AB$? to meet the criteria, SAS? ($MO, \angle O, AB$), with $O = $ intersection between altitude and $AB$ – ESCM Jun 13 '18 at 03:10
Yes, use the Intercept theorem for that. And what is SAS? – John McClane Jun 13 '18 at 05:27
How you know that the altitude from $M$ to $AB$ will be $midpoint$ of $AB$ ? – ESCM Jun 14 '18 at 15:30
And with $SAS$ i mean to the criteria of triangle congruence, SIDE-ANGLE-SIDE – ESCM Jun 14 '18 at 15:31
$O$ will be the midpoint of $AB$ because $M$ is the midpoint of $AC$, $MO \parallel CB$ and the intercept theorem is true. – John McClane Jun 14 '18 at 21:51

score 1 · Answer 3 · answered May 22 '24 at 17:18

1

A median from a right angled triangle, bisects the side.

This triange when inscribed in a circle (which is possible as a circle passes through any three non-collinear points ) makes the opposite side to be the diameter.

Now, the mid-point bisects the diameter into two radii, and the median is essentially connecting the centre to a point on the circle [BM] , ( i.e a vertex of the triangle ) which makes the median a radius as well, the fundamental property of circles describe that all radii are equal,

Hence BM = AM.

answered May 22 '24 at 17:18

Oppenheimer

21

Your answer is essentially equal to abc's. – Gonçalo May 22 '24 at 18:49
@Gonçalo True, but I thought that I'd add more details.. – Oppenheimer May 23 '24 at 02:40

Proving that the median to the hypotenuse of a right triangle is equal to half of the hypotenuse

3 Answers3

Linked