Showing that $\displaystyle\int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2}dx = \pi\left (\sqrt{a^2+1}-1\right)$.

Question

How can I show that $\displaystyle\int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2}dx = \pi\left(\sqrt{a^2+1}-1\right)$?

Answer 1

Putting $x=a\sin\theta,dx=a\cos\theta d\theta$ and $x=\pm a,\theta=\pm\frac\pi2 $

$$\int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2}dx =\int _{-\frac\pi2}^{\frac\pi2}\frac{a^2\cos^2\theta}{1+a^2\sin^2\theta}d\theta$$ $$=\int _{-\frac\pi2}^{\frac\pi2}\frac{a^2\sec^2\theta}{(1+\tan^2\theta)(1+(a^2+1)\tan^2\theta)}d\theta$$ (Diving the numerator & the denominator by $\sec^4\theta$)

$$=\int _{-\infty}^{\infty}\frac{a^2}{(1+t^2)(1+(a^2+1)t^2)}dt$$ (Putting $\tan\theta = t$ as $\tan\theta=\pm\infty, t=\pm\frac\pi2$)

$$=\frac{a^2}{(a^2+1)}\int _{-\infty}^{\infty}\frac{1}{(1+t^2)(\frac1{(a^2+1)}+t^2)}dt$$

$$=\frac{\frac{a^2}{(a^2+1)}}{\left(1-\frac1{1+a^2}\right)}\left(\int _{-\infty}^{\infty}\frac1{(\frac1{(a^2+1)}+t^2)}dt-\int _{-\infty}^{\infty}\frac{1}{(1+t^2)}dt\right)$$ as $\frac1{(c+y)(b+y)}=\frac1{c-b}\frac{(c+y)-(b+y)}{(c+y)(b+y)}=\frac1{c-b}\left(\frac1{y+b}-\frac1{y+c}\right)$

$$=\left(\sqrt{1+a^2}\arctan (t\sqrt{1+a^2} )-\arctan t\right)_{-\infty}^{\infty}$$

So,$$\int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2}dx=(\sqrt{1+a^2}-1)\frac\pi2-\left\{-(\sqrt{1+a^2}-1)\frac\pi2\right\}=(\sqrt{1+a^2}-1)\pi$$

---

Observe that we have put $x=a\sin\theta$ and $\tan\theta = t\implies \left(\frac ax\right)^2- \left(\frac 1t\right)^2=\csc^2\theta-\cot^2\theta=1$

$\implies t^2=\frac{x^2}{a^2-x^2}\iff x^2=\frac{a^2t^2}{1+t^2}, a^2-x^2=\frac{a^2}{1+t^2}$

So, if we straight away take $t=\frac x{\sqrt{a^2-x^2}}$ (assuming $a>0$)

$$\frac{dt}{dx}=\frac1{\sqrt{a^2-x^2}}+x\left(\frac{-1}2\right)\frac1{(a^2-x^2)^{\frac32}}(-2x)=\frac{a^2}{(a^2-x^2)^{\frac32}}$$

$$\sqrt{a^2-x^2} dx=\frac{(a^2-x^2)^2dt}{a^2}=\frac{a^2dt}{(1+t^2)^2}$$

and if $x=\pm a,t=\frac{\pm a}0=\pm\infty$

So, $$\int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2}dx$$ becomes $$\int _{-\infty}^{\infty}\frac{a^2}{(1+t^2)(1+(a^2+1)t^2)}dt$$

Answer 2

$\newcommand{\Res}{\operatorname{Res}}$ Since the question was tagged complex-analysis, and nobody has given a solutions with purely complex methods, here goes.

Let $$ f(z) = \frac{(a^2-z^2)^{1/2}}{1+z^2}, $$ where $(a^2-z^2)^{1/2}$ denotes branch that is holomorphic on $\mathbb{C} \setminus [-a,a]$. (See this question for details.)

Next, let $\Gamma$ be a "dog bone" contour together with a large circle:

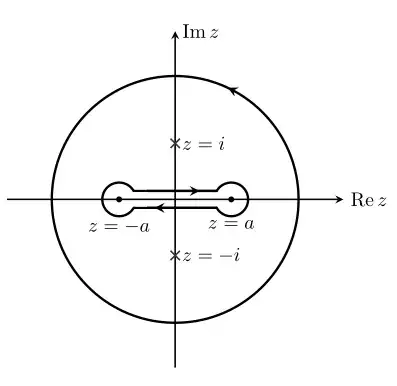
and integrate $f$ along $\Gamma$. On the "top" part of $[-a,a]$ we get the integral that we want. On the "bottom" part, the square root will pick up a minus sign from the branch cut and another minus sign from the orientation. It's straight forward to check that the integrals over the small circles tend to $0$ as their radii tend to $0$, and the integral over the large circle is basically the residue of $f$ at $\infty$. More precisely, by the residue theorem

\begin{align} 2\int_{-a}^a \frac{\sqrt{a^2-x^2}}{x^2+1}\,dx &= 2\pi i( \Res(f;i) + \Res(f;-i) - \Res(f;\infty)) \\ &= 2\pi i \bigg( \frac{\sqrt{a^2+1}}{2i} + \frac{-\sqrt{a^2+1}}{-2i} + i\bigg) \end{align}

which simplifies to the stated equality. (Note that $\Res(f;\infty) = \Res(-\dfrac1{z^2}f(\dfrac1z);0)$.)

Answer 3

A slight variant of lab bhattacharjee's method provides a simpler solution:

Let

$$ I(a) = \int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2} \, dx = 2\int_{0}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2} \, dx. $$

Then by a simple application of multivariable calculus,

\begin{align*} I'(a) &= 2 \left. \frac{\sqrt{a^2-x^2}}{1+x^2} \right|_{x=a} + 2 \int_{0}^{a} \frac{d}{da} \frac{\sqrt{a^2-x^2}}{1+x^2} \, dx \\ &= 2 \int_{0}^{a} \frac{a}{(1+x^2)\sqrt{a^2-x^2}} \, dx. \end{align*}

Then with the change of variable $x = a \sin\theta$, we have

\begin{align*} I'(a) &= 2 \int_{0}^{\frac{\pi}{2}} \frac{a}{1+a^2\sin^2\theta} \, d\theta \\ &= 2 \int_{0}^{\frac{\pi}{2}} \frac{a \sec^2\theta}{1+(a^2+1)\tan^2\theta} \, d\theta \\ &= 2 \int_{0}^{\infty} \frac{a}{1+(a^2+1)t^2} \, dt \qquad (t = \tan\theta) \\ &= \frac{\pi a}{\sqrt{a^2+1}}. \end{align*}

Thus by integrating, we must have

$$ I(a) = \pi\sqrt{a^2+1} + C $$

for some constant $C$. But

$$ I(0+) = \lim_{a\to0} \int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2} \, dx = \lim_{a\to0} \int_{-1}^{1} \frac{\sqrt{1-x^2}}{(1/a)^2+x^2} \, dx = 0 $$

and we must have $C = -\pi$. This proves the identity.

Answer 4

Let $x = a \sin(y)$. Then we have $$\dfrac{\sqrt{a^2-x^2}}{1+x^2} dx = \dfrac{a^2 \cos^2(y)}{1+a^2 \sin^2(y)} dy $$ Hence, $$I = \int_{-a}^{a}\dfrac{\sqrt{a^2-x^2}}{1+x^2} dx = \int_{-\pi/2}^{\pi/2} \dfrac{a^2 \cos^2(y)}{1+a^2 \sin^2(y)} dy $$ Hence, $$I + \pi = \int_{-\pi/2}^{\pi/2} \dfrac{a^2 \cos^2(y)}{1+a^2 \sin^2(y)} dy + \int_{-\pi/2}^{\pi/2} dy = \int_{-\pi/2}^{\pi/2} \dfrac{1+a^2}{1+a^2 \sin^2(y)} dy\\ = \dfrac{1+a^2}2 \int_0^{2 \pi} \dfrac{dy}{1+a^2 \sin^2(y)}$$ Now $$\int_0^{2 \pi} \dfrac{dy}{1+a^2 \sin^2(y)} = \oint_{|z| = 1} \dfrac{dz}{iz \left(1 + a^2 \left(\dfrac{z-\dfrac1z}{2i}\right)^2 \right)} = \oint_{|z| = 1} \dfrac{4z^2 dz}{iz \left(4z^2 - a^2 \left(z^2-1\right)^2 \right)}$$ $$\oint_{|z| = 1} \dfrac{4z^2 dz}{iz \left(4z^2 - a^2 \left(z^2-1\right)^2 \right)} = \oint_{|z| = 1} \dfrac{4z dz}{i(2z + a(z^2-1))(2z - a(z^2-1))}$$ Now $$ \dfrac{4z}{(2z + a(z^2-1))(2z - a(z^2-1))} = \dfrac1{az^2 - a + 2z} - \dfrac1{az^2 - a - 2z}$$ $$\oint_{\vert z \vert = 1} \dfrac{dz}{az^2 - a + 2z} = \oint_{\vert z \vert = 1} \dfrac{dz}{a \left(z + \dfrac{1 + \sqrt{1+a^2}}a\right) \left(z + \dfrac{1 - \sqrt{1+a^2}}a\right)} = \dfrac{2 \pi i}{2 \sqrt{1+a^2}}$$ $$\oint_{\vert z \vert = 1} \dfrac{dz}{az^2 - a - 2z} = \oint_{\vert z \vert = 1} \dfrac{dz}{a \left(z - \dfrac{1 + \sqrt{1+a^2}}a\right) \left(z - \dfrac{1 - \sqrt{1+a^2}}a\right)} = -\dfrac{2 \pi i}{2 \sqrt{1+a^2}}$$ Hence, $$\oint_{|z| = 1} \dfrac{4z dz}{i(2z + a(z^2-1))(2z - a(z^2-1))} = \dfrac{2 \pi i}i \dfrac1{\sqrt{1+a^2}} = \dfrac{2 \pi}{\sqrt{1+a^2}}$$ Hence, we get that $$I + \pi = \left(\dfrac{1+a^2}2\right) \dfrac{2 \pi}{\sqrt{1+a^2}} = \pi \sqrt{1+a^2}$$ Hence, we get that $$I = \pi \left(\sqrt{1+a^2} - 1 \right)$$

Answer 5

You can also convert it into an integral over the upper half-disk $D_a$ of radius $a$: $$\int_{D_a} {1 \over 1 + x^2}\,dy\,dx$$ (Do the $y$ integral first to convert it into the original form.) Since the integrand is even, it is twice the integral over the portion where $x > 0$. Changing to polar coordinates, this becomes $$2\int_0^a \int_0^{\pi \over 2} {r \over 1 + r^2\cos^2(\theta)}\,d\theta\,dr$$ $$= 2\int_0^a r \int_0^{\pi\over 2} {\sec^2(\theta) \over \sec^2(\theta) + r^2}\,d\theta\,dr$$ $$= 2\int_0^a r \int_0^{\pi\over 2} {\sec^2(\theta) \over \tan^2(\theta) + (1 + r^2)}\,d\theta\,dr$$ Doing a $u$ substitution this becomes $$= 2\int_0^a r \int_0^{\infty} {1 \over u^2 + (1 + r^2)}\,du\,dr$$ $$= 2\pi\int_0^a r {1 \over \sqrt{1 + r^2}}\,dr$$ $$=\pi \sqrt{1 + r^2}\,\,\,\bigg|_{r = 0}^{r = a}$$ $$=\pi\sqrt{1 + a^2} - \pi$$

Answer 6

Here's an elementary solution using only one substitution: Let $x=\frac{at}{\sqrt{1+t^2}}$ so that $$\begin{split}I& =\int_{-a}^a \frac{\sqrt{a^2-x^2}}{1+x^2}\, dx \\ &=\int_{-\infty}^{\infty}\frac{a^2}{(1+(1+a^2)t^2)(1+t^2)}dt \\ &=\int_{-\infty}^{\infty}\left(\frac{1+a^2}{1+(1+a^2)t^2}-\frac{1}{1+t^2}\right)\, dt \\ & =\pi\left(\sqrt{1+a^2}-1\right)\end{split}$$

Answer 7

Let $a=\tan \theta$ and substitue $ x =\frac{t\tan \theta}{\sqrt{t^2 +\sec \theta }}$

\begin{align} &\int_{-a}^{a} \frac{\sqrt{a^2-x^2}}{1+x^2}dx=\int_{0}^{\infty} \frac{2\sqrt{ \sec \theta }\ \tan^2\theta}{(t^2+ \frac1{t^2} ) \sec \theta +(1+ \sec^2\theta )}\overset{t\to \frac1t}{{d}t}\\ = &\int_{0}^{\infty}\frac{\sqrt{ \sec \theta }\ \tan^2\theta \ d(t-\frac1{t} )}{(t-\frac1{t} )^2 \sec \theta +(1+ \sec \theta )^2} ={\pi}( \sec \theta -1) = \pi\left(\sqrt{a^2+1}-1\right) \end{align}