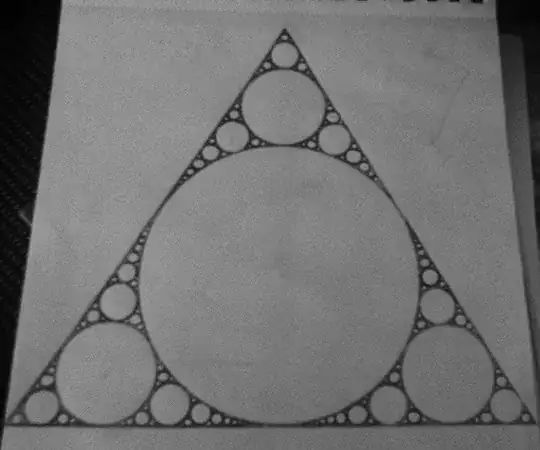
This is a semi-popular doodleing thing people do when they have a pen, paper and some time
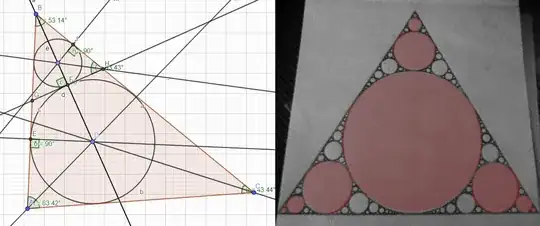
I want to construct one of these mathematically, and I got to a point where I'm able to find the coordinates of the triangles I marked on the right using the method on the left
But I have no idea how to construct the other ones.
I know everything about the triangle.
To compute the coordinates and radius of a particular circle, you need to start from the outermost triangle, recursively descend to the target circle and compute the coordinates/radii of intermediate circles along the way.
You essentially need to figure out following 4 things.
Given a triangle, how to find the incircle.
This is standard euclidean geometry. I won't repeat it here.
Given a pair of lines and a circle tangent to both lines, how to find an extra circle touching the two lines and circle.
It seems you have figured that out.
Given three circles tangent to each other, how to find an extra circle touching all three circles.
Let says we have 3 circles $C_1, C_2, C_3$ tangent to each other and $C_4$ is the extra circle in the hole formed by $C_1,C_2,C_3$ touching $C_1, C_2, C_3$. For each circle $C_i$, let $p_i = (x_i,y_i)$ and $r_i$ be its center and radius. Let $k_i = \frac{1}{r_i}$ be the curvature and $u_i = k_i p_i = \left(\frac{x_i}{r_i},\frac{y_i}{r_i}\right)$.
Descartes theorem tell us $$\begin{align} & (k_1 + k_2 + k_3 + k_4)^2 = 2(k_1^2 + k_2^2 + k_3^2 + k_4^2)\\ \implies & k_4 = k_1 + k_2+k_3 \pm 2\sqrt{k_1k_2 + k_2k_3 + k_3k_1}\end{align}$$ The '+' sign corresponds to circle $C_4$. The '-' sign is for the outer circle which encloses and touches $C_1, C_2, C_3$.
Once $k_4$ is determined, one can compute $u_4$ and hence $p_4$ using follow relation: $$\sum_{i=1}^4(k_t - 2k_i) u_i = 0 \implies u_4 = -\frac{1}{k_t - 2k_4}\sum_{k=1}^3(k_t - 2k_i)u_i\tag{*1}$$ where $k_t = \sum_{i=1}^4 k_i$. This relation is a special case of something I have proved before in an answer to a related question (look at Part II there).
Given a line $\ell_1$ and two circles $C_2, C_3$ tangent to each other, how to find an extra circle $C_4$ touching the line and two circles.
It turns out we can reuse formula $(*1)$. One just need to set $k_1$ to $0$ and $u_1$ to the unit normal vector of line $\ell_1$ pointing away from the circles. You can prove this yourself by first approximating the line $\ell_1$ by a circle $C_1$ with large radius $r_1$ and then send $r_1 \to \infty$.
