proofwiki.org?

Asked Jun 09 '18 at 12:33

Active Jun 10 '18 at 17:12

Viewed 289 times

I read the proof from https://proofwiki.org/wiki/Hall%27s_Marriage_Theorem/General_Set.

Here are screenshots from that link:

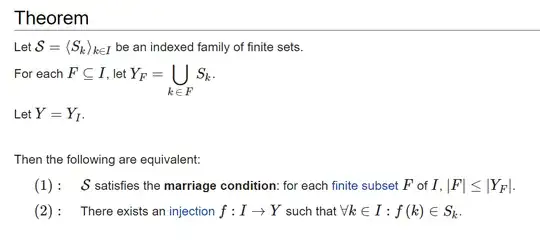
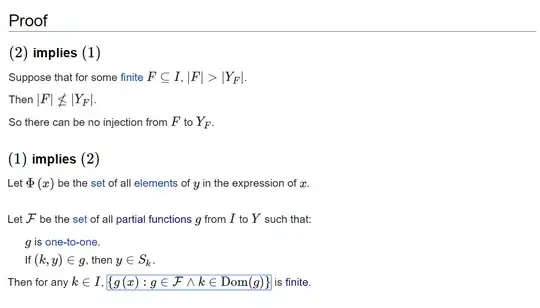
I suspect that the statement

Then for any $k\in I$, $\left\{ {g \left({x}\right): g \in \mathcal F \land k \in \operatorname{Dom} \left({g}\right)}\right\}$ is finite

is possibly not correct.

My reasoning: If $I$ is infinite, then for any $k$, it is possible that the number of function $g$ such that $g \in \mathcal F$ and $k \in \operatorname{Dom} \left({g}\right)$ is infinite by adding a new element from $I$ to the domain of existing function $g$.

Please check if my spot is correct! Thank you so much!

edited Jun 10 '18 at 17:12

asked Jun 09 '18 at 12:33

Akira

18,439

1

I tend to agree with you. – Arnaud Mortier Jun 09 '18 at 15:43
3

This is not a set of functions $g$; this is a set of values $g(x)$ which we get by evaluating a set of functions $g$ at some value $x$. Now, the proof doesn't tell us what $x$ is, so it doesn't make any sense, but it's possible that if $x$ were defined, the statement would be true. – Misha Lavrov Jun 10 '18 at 18:27
Yes, that part is too ambiguous. – Akira Jun 11 '18 at 00:06
1

If you're claiming the statement is incorrect, you should provide a counterexample. – Matthew Leingang Aug 17 '18 at 19:05

Is this a mistake in the proof of Hall's Marriage Theorem from https://proofwiki.org?

0 Answers0

Linked