0

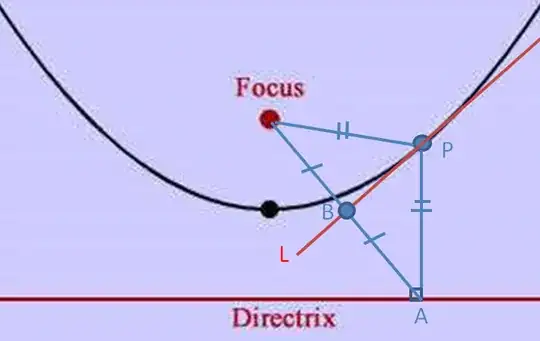
I have a parabola with the focus $F$ and the directrix $D.$ For a point $P$ on the parabola I constructed a triangle $FPA,$ where $A$ is the point where the perpendicular from $P$ to $D$ cuts $D.$ Search the midpoint of the segment $FA$ and name it $B.$ Then draw the line $L$ through $P$ and $B.$

enter image description here

I want to show that this last line $L$ is the tangent to the parabola in $P.$ (I have no equations or coordinates) what do I have to check? How can I do it without using the equation of the parabola and the coordinates of the point $P?$

Thank your for your help!

Adrian Keister
  • 10,272
mathlearner
  • 3
  • Welcome to MSE. Please, use MathJax to format your question: https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference. Importantly, show us you made an effort if you want to improve your chances of obtaining an answer – Green.H Jun 04 '18 at 14:52

1 Answers1

1

As in the image you added, $PA = PF$ by definition of parabola, where $F$ is the focus of the parabola.

Then, since by construction, $FB = AB$, we have that $\Delta PBF \cong \Delta PBA(PB \text{ is common to both})$ which implies $\angle FPB = \angle APB$, which is the necessary and sufficient condition for $PB$ to be a tangent, by the well-known Tangent Bisection Property (or See here)

ab123
  • 2,539