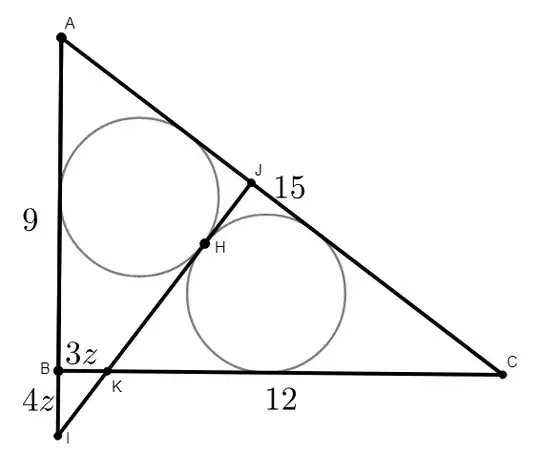
My attention was brought to a sangaku problem in this book by Ubukata Tou. It shows this figure:

The question asks us to find the diameter of the circles (both circles are congruent) in a right triangle ($∠ABC = 90$), where $AB = 9$ and $BC = 12$. It also says that the diameter of the two circles is $30/7$. How would you solve this problem. In the book, it also states that this was a problem from the early Edo period suggesting that trigonometry may not have been around in Japan then. It would be very interesting to see a solution without the use of trigonometry then.