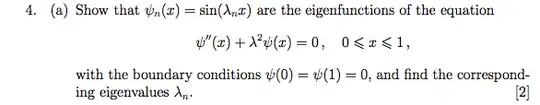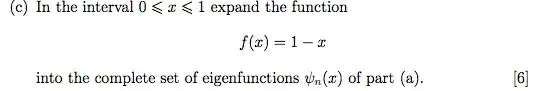1

I'm not sure how to use the bbcode so I've taken a screenshot instead:

enter image description here

Came up on a past exam paper that I'm working towards and I'm not sure how to answer it.

I assumed that EQN . EIGENFUNCTION = EIGENVECTOR . EIGENFUNCTION (from ef definition)

But it doesn't cancel out to a constant for eigenvector value.

Appreciate any help!

Endnote: The question continues:

enter image description here

And I'm not 100% sure about that either.

Again, thank you!

George Pearce
  • 113

2 Answers2

1

$$(\sin\lambda_nx)'=\lambda_n\cos\lambda_nx$$

$$(\sin\lambda_nx)'=-\lambda_n^2\sin\lambda_nx$$

So putting $\,\psi(x):=\sin\lambda_nx\,$ , we easily find the above are solutions to the given differential equation, and in order to have $\,\psi(1)=0\,$ we must choose $\,\lambda_n=k_n\pi\,\,,\,\,k_n\in\Bbb Z\,$

DonAntonio
  • 214,715
1

The eigenfunctions result from the boundary conditions. The generic solution to the differential equation is

$$ \psi(x) = A \cos{\lambda x} + B \sin{\lambda x} $$

We then apply the boundary condition $\psi(0) = 0$ and get

$$A \cos{0} + B \sin{0} = A = 0$$

The boundary condition $\psi(1) = 0$ implies that

$$B \sin{\lambda} = 0$$

We assume that $B \ne 0$. This latter equation puts a condition on the values of $\lambda$:

$$\sin{\lambda} = 0 \implies \lambda = n \pi \; \forall n \in \mathbb{Z}$$

We then may define $\lambda_n = n \pi$ as an eigenvalue of the differential operator defined above (the equation plus the boundary conditions). The general solution to this equation is a linear combination of eigenfunctions, that is, $\psi_n(x) = \cos{\lambda_n x}$.

By the way, maybe I am missing something, but (c) makes no sense to me, as $1-x$ does not satisfy the boundary conditions satisfied by the eigenfunctions $\psi_n(x)$.

Ron Gordon
  • 141,538
  • I think you should have $\psi(1)=B\sin\lambda$, where you have $\cos$. – Daryl Jan 15 '13 at 23:17
  • 1
    Already fixed it, but thanks anyway. – Ron Gordon Jan 15 '13 at 23:18
  • @iampearce: Does my concern about (c) make sense to you? Not sure how one expands $1-x$ over $[0,1]$ using those eigenfunctions to make any sensible approximation. – Ron Gordon Jan 15 '13 at 23:22
  • It does, but unfortunately I can't get hold of the tutor who set the exam in order to query it. I will ask as soon as I can, though - thank you again for your help. – George Pearce Jan 15 '13 at 23:34