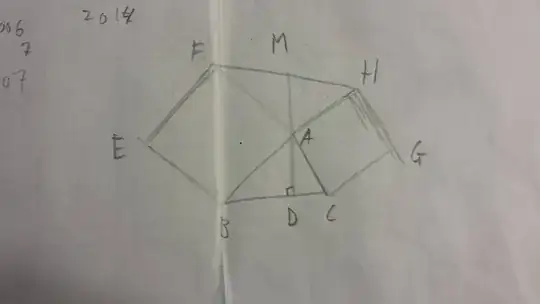
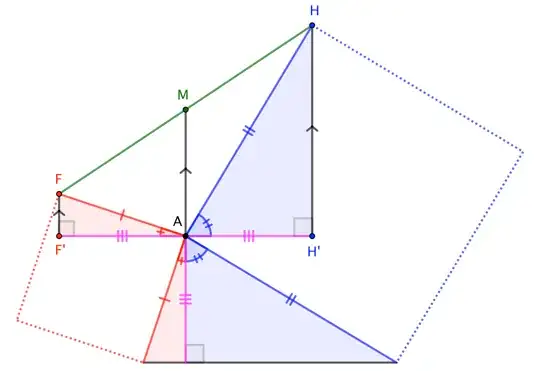
We start with $\triangle ABC$ with $AD$ as its altitude. We then construct squares $\square ABEF$ and $\square ACGH$ outwards from $AB$ and $AC$. We then connect $F$ and $H$. $DA$ is extended so it intersects $FH$ at $M$. How do we prove that $FM$ = $MH$?
I tried proving that $\triangle FAH$ is similar or congruent to $\triangle ABC$ but the angles don't match. I tried connecting $FD$ and $HD$ to form $\triangle FDH$ but I don't know how to proceed from there. I also tried connecting $FB$ and $HC$ to form $FBCH$ but I'm not sure if this helps. Am I missing something?