11

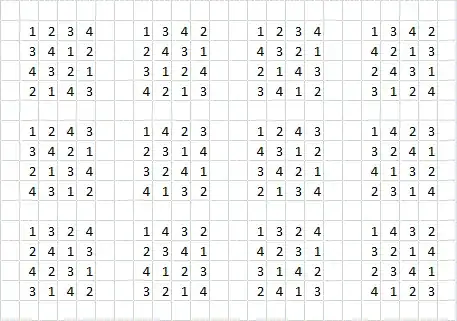
In how many ways can a $4 \times 4$ square grid be coloured using four different colours so that no colour is repeated in any row, column, or along the two main diagonals. For clarity, one valid solution to this problem is shown below.

enter image description here

I am after unique solutions, so:

  1. rotations of the grid through angles of $90^\circ, 180^\circ$, and $270^\circ$, and
  2. reflections about the horizontal, vertical, and the two main diagonals

are not considered different.

I am guessing this problem is perhaps well known, so I apologise in advance, but have not been able to make much progress towards its solution. It may even go by a well known name, making it easier to identify, and if this is indeed the case I would be interested in knowing what it is called.

omegadot
  • 12,364
  • So reflections are not count right? – user061703 Apr 27 '18 at 06:12
  • Yes, I should have added this. No reflections either. – omegadot Apr 27 '18 at 06:16
  • 1
    All different rotations and reflections of one grid must be unequal because all the corner tiles must have different colours. So the number of different colourings with rotations/reflections considered distinct is 8 times the binder of colourings with them considered not distinct. I think it's easiest to count of we first consider them distinct. – Arthur Apr 27 '18 at 06:17
  • 1
    This might help you. – Bergson Apr 27 '18 at 06:17
  • First, there are 16 ways to paint with one colour. once this color is chosen, now we have 6 remaining spots to paint with the other colours, pick one and then for the third one only 2 spots are available. We have then $16 \cdot 6 \cdot 2 $ ways to paint – James Apr 27 '18 at 06:19
  • Do you want to count different permutations of colors or not? For example, if we switch all of the red and yellow tiles, is this a new diagram? – Peter Kagey Apr 27 '18 at 06:32
  • This appears related to questions about equivalence classes of Latin squares. – Peter Kagey Apr 27 '18 at 06:35
  • Yes. Switching for example, the red and yellow tiles would be a different diagram. – omegadot Apr 27 '18 at 06:37
  • If you really want unique solutions then you could consider any pair of squares that only different by exchanging 2 colors to be indistinguishable. – DanielV May 05 '18 at 19:28

1 Answers1

8

Your requirements for the placement of colors is equivalent to the requirements for a diagonal Latin square, or as it used to be called, a double diagonal Latin square. According to OEIS, there are just $48$ diagonal Latin squares of order $4$, i.e. of size $4$ x $4$.

As @Arthur pointed out, if rotations and reflections are not considered distinct, we must divide this number by $8$. Hence, there are just $6$ distinct solutions.

EDIT

Just made a brute force program to check that I was right, and it gave the answer $12$, not $6$. Manual checking of the program's answer seems to show the program is correct. Here is the program's answer:

enter image description here

None of these appear to be rotations or reflections of each other. What did I miss?

EDIT 2

As @omegadot points out, the solutions above include reflections about the main diagonals. Removing these cases gives the following:

enter image description here

Jens
  • 5,786
  • 2
    Reflections about the main diagonals. For example, the two squares appearing in the top left corner are reflections of each other about the main diagonal running from the top left to bottom right. Remove these and you will get your 6. Great solution by way! – omegadot Apr 27 '18 at 13:21
  • @omegadot: Thanks! Reflections now removed. – Jens Apr 27 '18 at 18:46