The average energy of a free electron gas can be modeled as $$\epsilon=\frac{\int_0^\infty\frac{E^{3/2}dE}{\exp(E-\eta)+1}}{\int_0^\infty\frac{E^{1/2}dE}{\exp(E-\eta)+1}}$$
where $$\eta=\mu(T)/(k_B T)$$ $\mu(T)$ is the chemical potential which can be regarded as a constant.
Is there a way to obtain $T$ numerically in principal? I do know how to evaluate the fermi-integrals as well as their inverse if it helps.
This is a possible solution if you're familiar with python. There's a relation (at the time of writing this answer there is problem with this wiki entry, the argument of the polylog function is wrong) between the Fermi integral and the Polylogarithm:
$$ F_{s}(x)={\frac {1}{\Gamma (s+1)}}\int _{0}^{\infty }{\frac {t^{s}}{e^{t-x}+1}}\,dt = -{\rm Li}_{s+1}(-e^{x}) \tag{1} $$
This means
$$ \int _{0}^{\infty }{\frac {t^{s}}{e^{t-x}+1}}\,dt = -{\Gamma (s+1)} {\rm Li}_{s+1}(-e^{x}) \tag{2} $$
This a small script to calculate the average energy given a value of $\eta$
import mpmath
import scipy.optimize
# fermi-dirac integral
def fdint(s, eta):
result = -mpmath.gamma(s + 1) * mpmath.polylog(s + 1, -np.exp(eta))
return float('{}'.format(result.real))
# average energy from eta
def avge_eta(eta):
return fdint(1.5, eta) / fdint(0.5, eta)
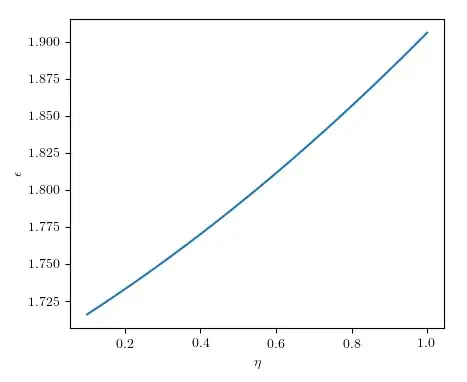
If you want to calculate $\eta$ (equivalently $T$) for a given value of $\epsilon$, add this function
# eta from average energy
def eta_avge(e):
f = lambda x: avge_eta(x) - e
results = scipy.optimize.newton(f, 1.0)
return np.real(results)
