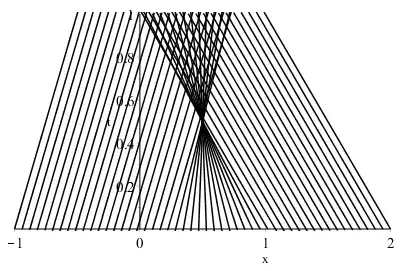
A good resource is Evan's book on PDE; he has a section on the method of characteristics. The basic idea is as follows. Given any suitable PDE with boundary conditions, we may turn this PDE into a series of ODE as follows. We pick a point $(x_0, 0)$ in the boundary (so here, the "boundary" is time $t = 0$). It would really be great if there were some path $y(s)$ connecting $(x_0, 0)$ to an arbitrary point $(x, t)$ in the interior (i.e. for time $t > 0$), and then set up an ODE along this path.
It turns out that for this specific PDE, what happens is that along this path $y$, the solution $u$ is constant. What this means is the following. Taken any $(x, t) \in \mathbb{R} \times (0, \infty)$. Then if we can connected $(x, t)$ to $(x_0, 0)$ along one of these characteristic curves $y$, we know that $u(x, t) = u(x_0, 0)$, since $u$ is constant on these curves.
Again, the general theory is helpful to see why, but that is a whole section in Evans' text. I will try to give a very brief introduction here.
Let $G(q, z, y)$ be a real-valued function. Into the variable $q$ here, we will input the tuple $(u_x, u_t)$; so $q$ represents the data of the gradient of $u$. The variable $z$ here will represent $u(x(s))$, where $x : I \to \mathbb{R} \times [0, \infty)$ is our characteristic curve (which is at this point unknown). The variable $y$ is just $y = (x, t)$. This function $G$ is the PDE function we are solving; that is, we are solving the equation $G = 0$. The general form of the characteristic equations that concern us now are
$$
\dot{z}(s) = q\cdot D_qG, \ \ \ \dot{x}(s) = D_qG.
$$
Well for this problem at hand, $G(q, z, y) =(1 - 2z, 1) \cdot q$, as
\begin{align*}
G(q, z, y) &= u_t + (1 - 2u)u_x \\
&= (1 - 2u, 1) \cdot (u_x, u_t) \\
&= (1 - 2z, 1)\cdot q.
\end{align*}
Thus, $D_qG$ is just the vector $(1 - 2z, 1)$. So the second characteristic equation is $\dot{x} = (1 - 2z, 1)$. So our characteristic curve $x$ satisfies this ODE.
Now the magic happens with $\dot{z}$, as this reduces to
$$
\dot{z}(s) = q\cdot D_qG = (u_x, u_t)\cdot (1 - 2z, 1) = 0;
$$
this is zero, remember, because this is exactly the PDE you are solving for! Since $z(s) = u(x(s))$, what this is literally saying is that the solution $u$ is constant (zero derivative!) along the characteristic curve $x$.
It is now a matter of integrating $\dot{z}$ along these curves to find the solution $u$. For a very good illustration of the method of characteristics, try solving the transport equation with constant coefficients, also in Evans.
As for shocks, I'll just suggest Evans, since this answer is already very long.