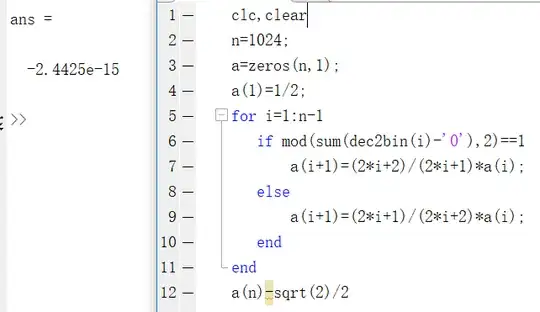
$a_1=\frac{1}{2},a_2=\frac{\frac{1}{2}}{\frac{3}{4}},a_3=\frac{\frac{\frac{1}{2}}{\frac{3}{4}}}{\frac{\frac{5}{6}}{\frac{7}{8}}}$... Prove that $\lim\limits_{n\rightarrow \infty}{a_n}=\frac{\sqrt{2}}{2}$
Notice that if $\frac{i}{i+1}$ is a numerator, then $\frac{i+2^n}{i+1+2^n}$ is a denominator. Each pair of number which is numerator is different from the pair of number that minus $2^n$.
For example, we notice that $a_3=\frac{1}{2}\frac{4}{3}\frac{6}{5}\frac{7}{8}$ and $\frac{1}{2}\rightarrow 00,\frac{3}{4}\rightarrow 01,\frac{5}{6}\rightarrow 10,\frac{7}{8}\rightarrow 11$